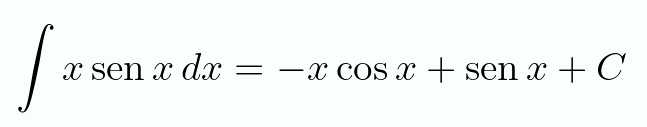Utilizando distintos métodos de integración se resuelven muchas integrales al nivel de 2º de Bachillerato Científico-Técnico (en la materia de Matemáticas II).
$$\int{\cos^2x\,dx=\begin{bmatrix}u=\cos x&\text{;}&du=-\text{sen}\,x\,dx\\dv=\cos x\,dx&\text{;}&v=\text{sen}\,x\end{bmatrix}}=$$
$$=\text{sen}\,x\cos x+\int{\text{sen}^2x\,dx}=\text{sen}\,x\cos x+x-\int{\cos^2x\,dx}\Rightarrow$$
$$2\int{\cos^2x\,dx}=x+\text{sen}\,x\cos x\Rightarrow\int{\cos^2x\,dx}=\frac{x+\text{sen}\,x\cos x}{2}+C$$
Hay otra forma más rápida de hacer esta integral, pero hemos de recordar una fórmula trigonométrica:
$$\cos 2x=\cos^2x-\text{sen}^2x\Rightarrow\cos 2x=\cos^2x-(1-\cos^2x)\Rightarrow$$
$$\Rightarrow\cos2x=2\cos^2x-1\Rightarrow\cos^2x=\frac{\cos2x+1}{2}$$
Entonces:
$$\int{\cos^2x\,dx}=\int{\frac{\cos2x+1}{2}\,dx}=\int{\frac{1}{2}\,dx}+\int{\frac{\cos2x}{2}\,dx}\Rightarrow$$
$$\Rightarrow\int{\cos^2x\,dx}=\frac{x}{2}+\frac{\text{sen}\,2x}{4}+C=\frac{x+\text{sen}\,x\cos x}{2}+C$$
Utilizando lo anterior:
$$\int{\text{sen}^2x\,dx}=\int{(1-\cos^2x)\,dx}=\int{1\,dx}-\int{\cos^2x\,dx}\Rightarrow$$
$$\int{\text{sen}^2x\,dx}=x-\frac{x+\text{sen}\,x\cos x}{2}+C=\frac{x-\text{sen}\,x\cos x}{2}+C$$
Otra integral fácil de hacer por partes es la siguiente:
$$\int{x\cos x\,dx}=\begin{bmatrix}u=x & \text{;} & du=dx\\dv=\cos x\,dx&\text{;}&v=\text{sen}\,x\end{bmatrix}=$$
$$=x\,\text{sen}\,x-\int{\text{sen}\,x\,dx}\Rightarrow\int{x\cos x\,dx}=x\,\text{sen}\,x+\cos x+C$$
De manera completamente análoga a la anterior:
$$\int{x\,\text{sen}\,x\,dx}=-x\cos x+\text{sen}\,x+C$$
Y, de momento, la última. Esta es inmediata:
$$\int{\text{sen}\,x\cos x\,dx}=\frac{\text{sen}^2x}{2}+C$$
Seguiremos en Integrales indefinidas. Cálculo de primitivas (II).