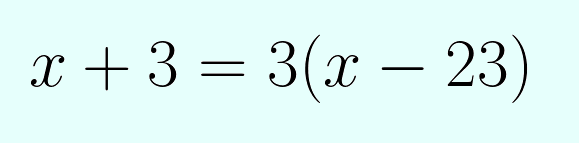El que puede cambiar sus pensamientos, puede cambiar su destino

Stephen Crane

---

En la Educación Secundaria Obligatoria, es muy habitual proponer la resolución de problemas mediante el planteamiento de ecuaciones de primer grado. Se propone a continuación un problema de este tipo.

Enunciado

Un niño es 26 años menor que su padre. Dentro de tres años, la edad del padre será el triple que la del hijo. ¿Cuántos años tiene cada uno en la actualidad?

Solución

Llamemos $x$ a la edad del padre en la actualidad. Entonces la edad del hijo es $x-26$ años, ya que es 26 años menor que su padre. Una vez fijadas estas dos edades, la edad de cada uno dentro de tres años será: $x+3$ años la del padre, y $x-26+3=x-23$ años la del hijo. A veces es bueno escribir la información en una tabla:

$$\begin{array}{|ccc|}\hline & \text{En la actualidad}& \text{Dentro de tres años}\\ \text{Edad del padre}& x& x+3\\ \text{Edad del hijo}& x-26& x-26+3=x-23\\ \hline\end{array}$$

Pero, según se dice en el enunciado, dentro de tres años la edad del padre será el triple que la edad del hijo. Y esto, en lenguaje matemático, lo podemos escribir así:

$$x+3=3(x-23)$$

Acabamos de plantear una ecuación de primer grado con los datos del problema. Ahora basta con resolverla e interpretar la solución.

$x+3=3\left(x–23\right)\Rightarrow x+3=3x–69\Rightarrow$

$\Rightarrow x–3x=–69–3\Rightarrow –2x=–72\Rightarrow x={\displaystyle \frac{–72}{–2}}\Rightarrow x=36$

Por tanto, el padre tiene, en la actualidad, 36 años (recuérdese que habíamos llamado $x$ a la edad actual del padre). Como la edad del hijo en la actualidad es $x-26$ años, sustituyendo el valor de $x$, se tiene que $x-26=36-26=10$. Es decir, la edad del hijo actualmente será de 10 años.

Ahora podemos comprobar que los resultados obtenidos se ajustan al enunciado.

• Como el padre tiene 36 años y el hijo 10 años, está claro que el hijo es 26 años menor que su padre.
• También es claro que, dentro de tres años, el padre tendrá 39 años y el hijo tendrá 13 años. Pero resulta que $39=3\cdot 13$. Por tanto, se cumple que dentro de tres años la edad del padre será el triple que la edad de su hijo.