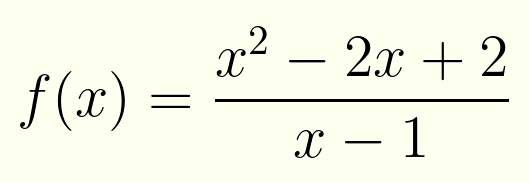Vamos a hacer un estudio bastante completo de una función racional. Hallaremos su dominio, sus puntos de corte con los ejes y sus asíntotas. También estudiaremos su monotonía (intervalos de crecimiento y decrecimiento), así como sus extremos (máximos y mínimos) relativos.
Recordemos que una función racional es una función como la siguiente:
$$f(x)=\frac{p(x)}{q(x)}$$
donde $p(x)$ y $q(x)$ son polinomios.
Por ejemplo, la función
$$f(x)=\frac{x^2-2x+2}{x-1}$$
se trata de una función racional, y ésta será la función objeto de nuestro estudio.
Dominio
Es fácil darse cuenta de que el denominador de la función se anula para $x=1$. Entonces:
$$\text{Dom}\,f=\mathbb{R}-\{1\}$$
Puntos de corte con los ejes
Los puntos de corte con el eje $X$ son de la forma $(x,0)$. Por tanto, para obtenerlos habremos de resolver la ecuación $f(x)=0\Leftrightarrow\dfrac{x^2-2x+2}{x-1}=0$.
Pero un cociente es cero si el numerador es cero. luego habremos de resolver la ecuación $x^2-2x+2=0$, ecuación de segundo grado que no tiene solución real porque su discriminante es menor que cero: $\Delta=(-2)^2-4\cdot1\cdot2=4-8=-4$.
Por tanto, la gráfica de nuestra función no corta al eje $X$.
Los puntos de corte con el eje $Y$ son de la forma $(0,y)$. Entonces, haciendo $x=0$, obtenemos claramente que $y=-2$. Esto quiere decir que la gráfica de la función corta al eje $Y$ en el punto $(0,-2)$.
Asíntotas
Una recta vertical $x=k$ es una asíntota vertical de una función $f(x)$ si se cumple que
$$\lim_{x\rightarrow k}f(x)=\pm\infty$$
Para que esto pueda ocurrir debemos estudiar el límite en el punto que no pertenece al dominio, es decir, en $x=1$:
$$\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 2x + 2}}{{x – 1}} = \left[ {\frac{1}{0}} \right] = \left\{ \begin{array}{lcl} -\infty & \text{ si } & x\to1^- \\ +\infty & \text{ si } & x\to1^+ \\ \end{array} \right.$$
De lo anterior se deduce que $x=1$ es una asíntota vertical.
Una recta vertical $y=k$ es una asíntota horizontal de una función $f(x)$ si se cumple que
$$\lim_{x\to \pm\infty}f(x)=k$$
En nuestro caso:
$$\mathop {\lim }\limits_{x \to \pm\infty} \frac{{{x^2} – 2x + 2}}{{x – 1}} = \left\{ \begin{array}{lcl} +\infty & \text{ si } & x\to+\infty \\ -\infty & \text{ si } & x\to-\infty \\ \end{array} \right.$$
Esto ocurre porque el grado del polinomio del numerador es mayor que el grado del polinomio del denominador. Como el límite en el infinito de la función no es un número real, hemos de deducir que $f$ no tiene asíntotas horizontales.
Una recta de la forma $y=mx+n$ es una asíntota oblicua de una función $f$ si
$$m=\lim_{x\to\pm\infty}\frac{f(x)}{x}\quad;\quad n=\lim_{x\to\pm\infty}\left(f(x)-mx\right)$$
En este caso tenemos:
$$m=\lim_{x\to\pm\infty}\frac{f(x)}{x}=\lim_{x\to\pm\infty}\frac{x^2-2x+2}{x^2-x}=1$$
$$n = \mathop {\lim }\limits_{x \to \infty } \left( {f\left( x \right) – mx} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} – 2x + 2}}{{x – 1}} – x} \right) =$$
$$= \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} – 2x + 2}}{{x – 1}} – \frac{{{x^2} – x}}{{x – 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } \frac{{ – x + 2}}{{x – 1}} = \frac{{ – 1}}{1} = – 1$$
De lo anterior se deduce que $y=x-1$ es una asíntota oblicua de la función.
Extremos (máximos y mínimos) y monotonía: intervalos de crecimiento y decrecimiento
Si una función $f$ presenta en un punto $x=a$ un máximo o un mínimo relativo, entonces se tiene que $f'(a)=0$. Derivemos pues nuestra función e igualemos a cero.
Usando la regla de derivación de un cociente:
$$f'(x)=\frac{(2x-2)\cdot(x-1)-(x^2-2x+2)\cdot1}{(x-1)^2}=$$
$$=\frac{2x^2-2x-2x+2-x^2+2x-2}{x-1}=\frac{x^2-2x}{(x-1)^2}$$
Entonces
$$f'(x)=0\Leftrightarrow x^2-2x=0\Leftrightarrow x=0\ \text{;}\ x=2$$
Estos dos puntos reciben el nombre de puntos singulares o críticos, a los que vamos a añadir el punto $x=1$ (que no pertenecía al dominio) para elaborar una tabla en la que estudiar el crecimiento y el decrecimiento de la función. Recordemos antes que si $f'(a)>0$, entonces $f$ es creciente en $x=a$, y que si $f'(a)<0$, entonces $f$ es decreciente $x=a$.
$$ \begin{array}{||c|c|c|c|c||} \hline \hline & (-\infty,0) & (0,1) & (1,2) & (2,+\infty)\\\hline f’ & + & – & – & +\\\hline f & \uparrow \uparrow& \downarrow\downarrow & \downarrow\downarrow & \uparrow\uparrow\\\hline \hline\end{array} $$
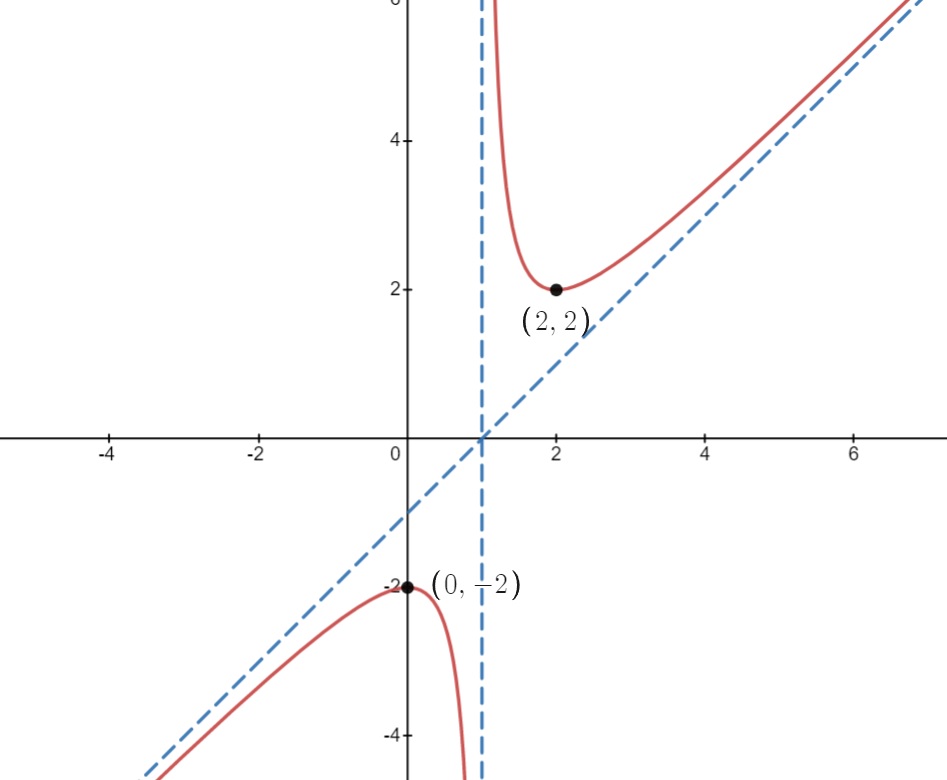
Por tanto, $f$ es creciente en $(-\infty,0)\cup(2,+\infty)$ y decreciente en $(0,1)\cup(1,2)$. Además, tiene un mínimo relativo en el punto $(0,-2)$ y un máximo relativo en el punto $(2,2)$.
Con todos los datos anteriores no es difícil esbozar la gráfica de la función. Es la siguiente: