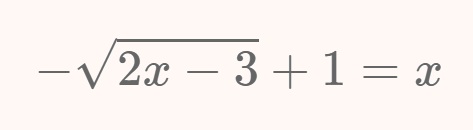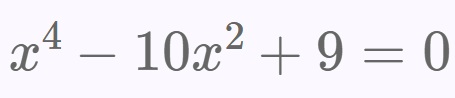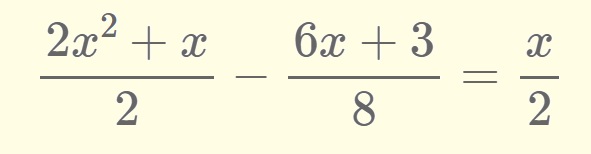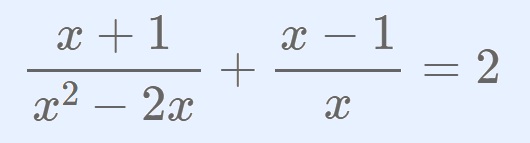En la vida hay algo peor que el fracaso: el no haber intentado nada
Franklin Delano Roosevelt
Por definición, el rango de una matriz es igual al número de filas linealmente independientes. Como en estos apuntes no vamos a hablar de independencia lineal, vamos a usar los determinantes para calcular el rango de una matriz. Antes, es necesario que hagamos algunas definiciones.
Submatrices y menores
Supongamos que $A$ es una matriz de orden $m\times n$, es decir, con $m$ filas y $n$ columnas: $A\in\mathfrak{M}_{m\times n}$.
- Se llama submatriz de $A$ a cualquier matriz que se obtenga a partir de $A$ suprimiendo filas y columnas.
- Si una submatriz de $A$ es cuadrada de orden $k$, a su determinante se le denomina menor de orden $k$ de $A$.
- Al menor formado por las $k$ primeras filas y las $k$ primeras columnas de $A$ se le llama menor principal de orden $k$ y lo denotaremos por $\delta_k$. Nótese que, si $m=n$, es decir, si $A$ es cuadrada de orden $n$, entonces $\delta_n=|A|$.
Por ejemplo, dada la matriz $A=\begin{pmatrix}
2&1&-3&4\\
0&4&-4&5
\end{pmatrix}$, el menor principal de orden $2$ es $\delta_2=\begin{vmatrix}
2&1\\
0&4
\end{vmatrix}=8-0=8$.
Rango de una matriz
Sea $A\in\mathfrak{M}_{m\times n}$. El rango de la matriz $A$ es el mayor orden de los menores no nulos de $A$. Denotaremos por $r(A)$ al rango de la matriz $A$.
Propiedades del rango de una matriz
a) El rango de una matriz no varía si se intercambian entre sí dos filas o dos columnas.
b) Si una matriz $A$ tiene una fila o columna de ceros, el rango de coincide con el rango de la matriz que se obtiene al suprimir esa fila o esa columna.
c) El rango de una matriz no cambia si se suprime una fila o una columna que sea combinación lineal de las restantes.
d) El rango de una matriz es igual al de su traspuesta: $r(A)=r\left(A^t\right)$.
e) Si $A$ es una matriz de orden $m\times n$, se tiene que $r(A)\leq\text{min}\{m\ ,n\}$. Es decir, el rango siempre es menor o a lo sumo igual que el número más pequeño de entre estos dos: número de filas y número de columnas. Así, por ejemplo, si una matriz es de orden $3\times 5$, su rango será a lo sumo $3$.
Merece la pena detenerse con un ejemplo, sobre todo para dejar constancia de la propiedad c) y explicar lo que significa que una fila sea combinación lineal de las restantes. Consideremos la siguiente matriz:
$$A=\begin{pmatrix}
3&1&-1&-2&1\\ 5&-3&5&0&9\\ 0&0&0&0&0 \\ 1&-2&3&1&4\\
\end{pmatrix}$$
Como $A$ tiene una fila de ceros (la tercera), según la propiedad b), el rango de la matriz anterior es igual al rango de esta otra, la cual se obtiene de la anterior suprimiendo la fila de ceros:
$$B=\begin{pmatrix}
3&1&-1&-2&1\\ 5&-3&5&0&9\\ 1&-2&3&1&4\\
\end{pmatrix}$$
Llamemos $f_1$, $f_2$ y $f_3$ a la fila 1, fila 2 y fila 3, respectivamente, de la matriz anterior. Entonces $2f_3+f_1=f_2$:
$$2\begin{pmatrix}1&-2&3&1&4\end{pmatrix}+\begin{pmatrix}3&1&-1&-2&1\end{pmatrix}=$$
$$=\begin{pmatrix}2&-4&6&2&8\end{pmatrix}+\begin{pmatrix}3&1&-1&-2&1\end{pmatrix}=\begin{pmatrix}5&-3&5&0&9\end{pmatrix}$$
Esto quiere decir que la fila 2 es combinación lineal (o simplemente combinación) de la fila 3 y la fila 1. Por tanto, según la propiedad c), podemos suprimir la fila 2 de la matriz anterior, con lo que su rango será igual al de esta otra:
$$C=\begin{pmatrix}
3&1&-1&-2&1\\ 1&-2&3&1&4\\
\end{pmatrix}$$
Según la propiedad e), como esta matriz es de orden $2\times5$, su rango será, a los sumo $2$: $r(A)\leq2$. De hecho, su rango es dos porque el menor principal de orden dos de esta matriz es distinto de cero: $\delta_1=\begin{vmatrix}
3&1\\ 1&-2 \end{vmatrix}=7\neq0$. Por tanto, finalmente tenemos que $r(A)=r(B)=r(C)=2$.
Ejemplos de distintos casos
Antes de ver un método general para hallar el rango de una matriz a partir de sus menores, veamos algunos ejemplos del cálculo del rango de una matriz según el orden de ésta:
Caso 1
$A$ es una matriz cuadrada de orden dos: $A=\begin{pmatrix}a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{pmatrix}$.
En este caso el único menor de orden dos es el menor principal, es decir, el determinante de la propia matriz $A$: $\delta_1=|A|$.
a) Si $\delta_1=|A|\neq0$, entonces $r(A)=2$. Por ejemplo, si $A=\begin{pmatrix}1&-2\\ 8&6\\ \end{pmatrix}$, entonces $r(A)=2$, ya que $|A|=10\neq0$.
b) Si $\delta_1=|A|=0$, el rango ya no puede ser igual a dos porque no habrá ningún menor de orden dos distinto de cero. Entonces, o bien $r(A)=1$, si hay algún término distinto de cero, $r(A)=0$, si todos los términos de la matriz son cero, es decir, si $A$ se trata de la matriz nula. Por ejemplo, si $A=\begin{pmatrix}2&-5\\ -4&10\\ \end{pmatrix}$, entonces $r(A)=1$, porque $|A|=0$, y hay términos distintos de cero en la matriz. Observa que el determinante será nulo cuando las dos filas sean proporcionales. En este caso la fila 2 es igual a la fila 1 multiplicada por $2$.
Caso 2
$A$ es una matriz de orden $2\times3$: $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ \end{pmatrix}$.
En este caso, la matriz $A$ tiene tres menores de orden dos:
$$\begin{vmatrix}a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{vmatrix}\quad ; \quad\begin{vmatrix}a_{11}&a_{13}\\ a_{21}&a_{23}\\ \end{vmatrix}\quad; \quad\begin{vmatrix}a_{12}&a_{13}\\ a_{22}&a_{23}\\ \end{vmatrix}$$
Si alguno de ellos es distinto de cero, $r(A)=2$. Si todos son cero, entonces el rango será uno (cuando algún término de la matriz sea distinto de cero) o será cero (cuando $A$ sea la matriz nula).
Por ejemplo, el rango de la matriz $A=\begin{pmatrix}-1&2&-5\\ 4&-8&6\\ \end{pmatrix}$ es dos porque contiene un menor de orden dos distinto de cero: $\begin{vmatrix}-1&-5\\ 4&6\\ \end{vmatrix}=-6+20=14\neq0$. Obsérvese que el menor principal es igual a cero: $\begin{vmatrix}-1&2\\ 4&-8\\ \end{vmatrix}=8-8=0$. Seguramente, sería con el primero que probaríamos. Pero, al ser cero, seguimos probando con el resto. En cuanto demos con uno que sea distinto de cero (como ocurre en este caso), el rango de la matriz ya es dos.
Caso 3
$A$ es una matriz de orden $3\times2$. Entonces, como su traspuesta es de orden $2\times3$, por la propiedad d), $r(A)=r\left(A^t\right)$, y se procede como en el caso anterior.
Caso 4
$A$ es una matriz de orden $2\times m$, con $m>3$ En este caso se procede como en el caso 2, lo que ocurre es que habrá más menores de orden dos.
Caso 5
$A$ es una matriz de orden $n\times2$, con $n>3$. En este caso se procede como en el caso 3.
Caso 6
$A$ es una matriz cuadrada de orden tres: $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{31}\\ \end{pmatrix}$.
En este caso el único menor de orden tres es el menor principal, es decir, el determinante de la propia matriz $A$: $\delta_1=|A|$.
a) Si $\delta_1=|A|\neq0$, entonces $r(A)=3$. Por ejemplo, si $A=\begin{pmatrix}1&2&-2\\ 0&-4&-1\\ -2&1&1\\ \end{pmatrix}$, entonces tenemos que $r(A)=3$, ya que
$$|A|=\begin{vmatrix}1&2&-2\\ 0&-4&-1\\ -2&1&1\\ \end{vmatrix}=(-4+4+0)-(-16+0-1)=0-(-17)=17\neq0$$
b) Si $\delta_1=|A|=0$, el rango ya no puede ser igual a tres porque no habrá ningún menor de orden tres distinto de cero. Entonces $r(A)\leq2$.
Por ejemplo, consideremos la matriz $A=\begin{pmatrix}1&3&-4\\ -1&-1&2\\ 0&2&-2\\ \end{pmatrix}$. Se tiene que $|A|=0$ (¡compruébalo!). De hecho, la tercera fila es la suma de las dos primeras. Entonces su rango ya no es tres. Pero como hay al menos un menor de orden dos distinto de cero, su rango es dos:
$$|A|=\begin{vmatrix}1&3\\ -1&-1\\ \end{vmatrix}=-1-(-3)=-1+3=2\neq0\Rightarrow r(A)=2$$
Caso 7
$A$ es una matriz de orden $3\times4$: $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{31}&a_{34}\\ \end{pmatrix}$.
En este caso, la matriz $A$ tiene cuatro menores de orden tres:
$$\begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{31}\\ \end{vmatrix}\quad;\quad \begin{vmatrix}a_{11}&a_{12}&a_{14}\\ a_{21}&a_{22}&a_{24}\\ a_{31}&a_{32}&a_{34}\\ \end{vmatrix}\quad;\quad \begin{vmatrix}a_{11}&a_{13}&a_{14}\\ a_{21}&a_{23}&a_{24}\\ a_{31}&a_{33}&a_{34}\\ \end{vmatrix}\quad;\quad \begin{vmatrix}a_{12}&a_{13}&a_{14}\\ a_{22}&a_{23}&a_{24}\\ a_{32}&a_{33}&a_{34}\\ \end{vmatrix}$$
Si alguno de ellos es distinto de cero, $r(A)=3$. Si todos son cero, entonces $r(A)\leq2$.
Por ejemplo, consideremos la matriz $A=\begin{pmatrix}1&2&-1&-2\\ 3&0&1&-4\\ 1&-1&1&-1\\ \end{pmatrix}$.
Puede comprobarse que todos los menores de orden tres son nulos:
$$\begin{vmatrix}1&2&-1\\ 3&0&1\\ 1&-1&1\\ \end{vmatrix} = \begin{vmatrix}1&2&-2\\ 3&0&-4\\ 1&-1&-1\\ \end{vmatrix} = \begin{vmatrix}1&-1&-2\\ 3&1&-4\\ 1&1&-1\\ \end{vmatrix} = \begin{vmatrix}2&-1&-2\\ 0&1&-4\\ -1&1&-1\\ \end{vmatrix} = 0$$
Como $\begin{vmatrix}1&2\\ 3&0\\ \end{vmatrix}=0-6=-6\neq0$, se tiene que $r(A)=2$.
Caso 8
$A$ es una matriz de orden $4\times3$. Entonces, como su traspuesta es de orden $3\times4$, por la propiedad d), $r(A)=r\left(A^t\right)$, y se procede como en el caso anterior.
Caso 9
$A$ es una matriz de orden $3\times m$, con $m>4$. En este caso se procede como en el caso 7, lo que ocurre es que habrá más menores de orden tres.
Caso 10
$A$ es una matriz de orden $n\times3$, con $n>4$. En este caso se procede como en el caso 8.
Se han analizado especialmente estos casos porque se usarán para la resolución de muchos sistemas de ecuaciones lineales que aparecen con frecuencia en los exámenes.
Método general para hallar el rango de una matriz a partir de sus menores
Ya hemos visto anteriormente varios ejemplos de cálculo del rango de una matriz. La mejor forma de explicar el método general es hacerlo con otro ejemplo.
Supongamos que queremos hallar el rango de $A=\begin{pmatrix}-1&3&0&1&2\\ 0&5&1&2&3\\ -3&-1&-2&-1&0\\ 3&11&4&5&6\\ \end{pmatrix}$. Observa que el orden de la matriz $A$ es $4\times5$, con lo que $r(A)\leq4$.
En primer lugar, se busca un menor de orden dos no nulo. Por ejemplo, $\begin{vmatrix}-1&0\\ 0&1 \\ \end{vmatrix}=-1\neq0$. Esto asegura que el rango de $A$ ya es, al menos, dos. Obsérvese que el menor está formado por las filas 1 y 2, y las columnas 1 y 3. Ahora, con la tercera fila, calculamos todos los menores de orden tres que contengan al menor anterior. Son los siguientes:
$$\begin{vmatrix}-1&3&0\\ 0&5&1\\ -3&-1&-2\\ \end{vmatrix}=0\quad;\quad \begin{vmatrix}-1&0&1\\ 0&1&2\\ -3&-2&-1\\ \end{vmatrix}=0\quad;\quad \begin{vmatrix}-1&0&2\\ 0&1&3\\ -3&-2&0\\ \end{vmatrix}=0$$
Ahora hacemos los mismo que antes, pero con la cuarta fila. Los tres menores de orden 3 que así se obtienen son también iguales a cero (¡compruébese!).
Este método se conoce con el nombre de orlar un menor con menores de orden una unidad superior. Pues bien, es posible demostrar que, si todos los menores obtenidos de este modo son cero, el resto también lo son.
De aquí deducimos que $r(A)=2$ (mayor orden de los menores no nulos de $A$).
Si algún menor de orden tres fuese distinto de cero, el rango de la matriz sería al menos 3 y procederíamos a orlar con los de orden 4. Este método se repite sucesivamente hasta obtener el rango de la matriz $A$ como el mayor orden de los menores no nulos de $A$.
Normalmente, se comienza a orlar con el primer menor de orden dos disponible, caso de que este sea distinto de cero. En el ejemplo anterior, este menor es el formado por las dos primeras filas y las dos primeras columnas, es decir, el menor $\begin{vmatrix}-1&3\\ 0&5 \\ \end{vmatrix}=-5\neq0$. Ahora se puede comprobar que los seis menores de orden tres que lo contienen son iguales a cero (al igual que lo que ocurría anteriormente), con lo que el rango de la matriz es dos.
No será habitual que nos pidan calcular el rango de una matriz de orden superior a $4\times4$, como en el caso del ejemplo anterior. Para matrices de orden $4\times4$. deberemos de saber calcular determinantes de orden cuatro, pero eso lo dejaremos para otro momento.
Rango de matrices dependientes de un parámetro
Por último, haremos un par de ejemplos de cálculo del rango de matrices dependiendo de un parámetro.
Ejemplo 1
Calcular el rango de la matriz $B=\begin{pmatrix}t&t&0\\ 2&t+1&t-1\\ 2t+1&0&-t-3\\ \end{pmatrix}$, en función del parámetro $t$.
Como esta matriz es cuadrada de orden tres, tendrá rango tres si su determinante es distinto de cero. En caso contrario su rango será menor que tres. Pero todo ello dependerá de los valores que tome el parámetro $t$.
El determinante de la matriz $B$ es:
$$|B|=\begin{vmatrix}t&t&0\\ 2&t+1&t-1\\ 2t+1&0&-t-3\\ \end{vmatrix}=t\left( {t + 1} \right)\left( { – t – 3} \right) + t\left( {t – 1} \right)\left( {2t + 1} \right) – 2t\left( { – t – 3} \right)=$$
$$=t\left( {\left( {t + 1} \right)\left( { – t – 3} \right) + \left( {t – 1} \right)\left( {2t + 1} \right) – 2\left( { – t – 3} \right)} \right)=$$
$$=t\left( { – {t^2} – 4t – 3 + 2{t^2} – t – 1 + 2t + 6} \right) = t\left( {{t^2} – 3t + 2} \right)$$
Ahora podemos hallar los valores de $t$ para los cuales el determinante de $B$ es cero:
$$|B| = 0 \Leftrightarrow t(t^2 – 3t + 2) = 0 \Leftrightarrow \begin{cases} t = 0\\ t^2 – 3t + 2 = 0 \end{cases}$$
Pero
$${t^2} – 3t + 2 = 0 \Leftrightarrow t = \frac{{ – \left( { – 3} \right) \pm \sqrt {{{\left( { – 3} \right)}^2} – 4 \cdot 1 \cdot 2} }}{{2 \cdot 1}} = \frac{{3 \pm \sqrt {9 – 8} }}{2} = \frac{{3 \pm 1}}{2} = \begin{cases} t = 2\\ t = 1 \end{cases}$$
Resumiendo, $|B|=0$ si $t=0$, o $t=1$, o bien $t=2$.
De aquí ya podemos afirmar que si $t\neq0$, $t\neq1$ y $t\neq2$, entonces $|B|\neq0$, con lo que $r(B)=3$.
Si $t=0$, $B=\begin{pmatrix}0&0&0\\ 2&1&-1\\ 1&0&3\\ \end{pmatrix}$. Si $t=1$, $B=\begin{pmatrix}1&1&0\\ 2&2&0\\ 3&0&-4\\ \end{pmatrix}$. Si $t=2$, $B=\begin{pmatrix}2&2&0\\ 2&3&1\\ 5&0&-5\\ \end{pmatrix}$
En cualquiera de los casos se tiene que $r(B)=2$, porque en cada uno de los tres casos se pueden encontrar menores de orden dos distintos de cero.
Ejemplo 2
Se trataría de estudiar el rango de la matriz $A=\begin{pmatrix}a&1&3&0\\ 1&a&2&1\\ 2&2a&5&a\\ \end{pmatrix}$, según los valores del parámetro $a$.
Un menor de orden dos distinto de cero es $\begin{vmatrix}3&0\\2&1 \end{vmatrix}=3\neq0$. Esto quiere decir que el rango de $A$ al menos dos.
El menor anterior contiene dos menores de orden tres:
$$\begin{vmatrix}a&3&0\\ 1&2&1\\ 2&5&a \end{vmatrix}=2a^2-8a+6\quad;\quad \begin{vmatrix}1&3&0\\ a&2&1\\ 2a&5&a \end{vmatrix}=-3a^2+8a-5$$
Si ambos fueran igual a cero, el rango de la matriz $A$ no sería igual a tres, con lo que $r(A)=2$. Y si alguno de ellos fuera distinto de cero, entonces $r(A)=3$. Pero eso dependerá de los valores del parámetro $a$. Igualemos a cero ambos y veamos qué ocurre.
$$\begin{vmatrix}a&3&0\\ 1&2&1\\ 2&5&a \end{vmatrix}=2a^2-8a+6=0\Leftrightarrow a=\frac{-(-8)\pm\sqrt{(-8)^2-4\cdot2\cdot6}}{2\cdot2}=$$
$$=\frac{-(-8)\pm\sqrt{16}}{4}=\frac{-(-8)\pm4}{4}=\begin{cases}a_1=3\\a_2=1\end{cases}$$
$$\begin{vmatrix}1&3&0\\ a&2&1\\ 2a&5&a \end{vmatrix}=-3a^2+8a-5=0\Leftrightarrow a=\frac{-8\pm\sqrt{8^2-4\cdot(-3)\cdot(-5)}}{2\cdot(-3)}=$$
$$=\frac{-8\pm\sqrt{4}}{-6}=\frac{-8\pm2}{-6}=\begin{cases}a_1=1\\a_2=\frac{5}{3}\end{cases}$$
De lo anterior se desprende que él único valor común para el que los dos menores de orden tres es igual a cero, es $a=1$. Si $a$ toma cualquier otro valor, alguno de ellos será distinto de cero. Por tanto, podemos concluir lo siguiente.
Si $a=1$, $r(A)=2$. Y si $a\neq1$, $r(A)=3$.
Puedes ver y descargar este artículo en formato pdf aquí.