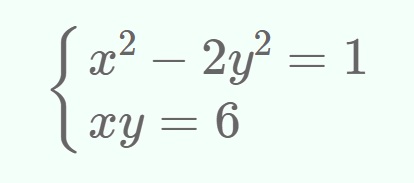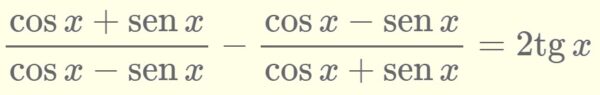El álgebra es generosa; siempre da más de lo que pide

Jean le Rond d’Alembert

---

Consideremos un sistema de \(n\) ecuaciones lineales con \(n\) incógnitas como el siguiente:

$$\left\{\begin{array}{c}a_{11}x_1+a_{12}x_2+\ldots+a_{1n}x_n=b_1 \\ a_{21}x_1+a_{22}x_2+\ldots+a_{2n}x_n=b_2 \\………………………… \\ a_{n1}x_1+a_{n2}x_2+\ldots+a_{nn}x_n=b_n \end{array}\right.$$

La matriz de los coeficientes y la matriz ampliada del sistema son las siguientes:

$$A=\left(\begin{array}{cccc}a_{11} & a_{12} & \ldots & a_{1n} \\a_{21} & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \ldots & a_{nn} \\ \end{array}\right)\quad;\quad A|b=\left(\begin{array}{cccc|c}a_{11} & a_{12} & \ldots &a_{1n} & b_1\\a_{21} & a_{22} & \ldots & a_{2n} & b_2\\ \vdots & \vdots & \ddots & \vdots & \vdots\\a_{n1} & a_{n2} & \ldots & a_{nn} & b_n\\ \end{array}\right)$$

Según el teorema de Rouché, si el rango de la matriz de los coeficientes es igual que el rango de la matriz ampliada el sistema es compatible. Si además, dicho rango coincide con el número de incógnitas, es decir, si \(r(A)=r(A|b)=n\), entonces el sistema es compatible determinado, o sea, que tiene solución única. La condición necesaria y suficiente para que se cumpla lo anterior es que el determinante de la matriz de los coeficientes sea distinto de cero, es decir:

$$|A|\neq0\Leftrightarrow r(A)=r(A|B)=n$$

En este caso, la solución del sistema viene dada por según una serie de identidades que se conocen con el nombre de regla de Cramer:

$$x_1=\frac{\left|\begin{array}{cccc}b_1 & a_{12} & \ldots & a_{1n} \\b_2 & a_{22} & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\b_n & a_{n2} & \ldots & a_{nn} \end{array}\right|}{|A|} , x_2=\frac{\left|\begin{array}{cccc}a_{11} & b_1 & \ldots & a_{1n} \\ a_{21} & b_2 & \ldots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\a_{n1} & b_n & \ldots & a_{nn}\end{array}\right|}{|A|},\ldots,x_n=\frac{\left|\begin{array}{cccc}a_{11} & a_{12} & \ldots & b_1 \\a_{21} & a_{22} & \ldots & b_2 \\ \vdots & \vdots & \ddots & \vdots \\a_{n1} & a_{n2} & \ldots & b_n\end{array}\right|}{|A|}$$

Obsérvese que, en la práctica, para obtener la incógnita \(x_i\) se dividen los valores de dos determinantes. El del numerador es el mismo que el de la matriz de los coeficientes, con la salvedad de que la columna \(i\) se sustituye por la columna de los términos independientes. El denominador es el determinante de la matriz de los coeficientes en todos los casos.

Veamos algunos ejemplos de aplicación de la regla de Cramer.

Ejemplo 1

Consideremos el siguiente sistema de ecuaciones:

$$\begin{cases}8x-6y+2z=-1\\3x+y-z=10\\-x+3y-2z=5\end{cases}$$

El determinante de la matriz de los coeficientes es:

$$|A|=\left|\begin{array}{ccc}8 & -6 & 2 \\3 & 1 & -1\\-1 & 3 & -2\end{array}\right|=(-16-6+18)-(-2+36-24)=-4-10=-14$$

Como el determinante anterior es distinto de cero el sistema es compatible determinando (rango de la matriz de los coeficientes, igual al rango de la matriz ampliada, igual a tres, que es el número de incógnitas). Aplicando la regla de Cramer obtenemos las soluciones:

$$x=\frac{\left|\begin{array}{ccc}-1 & -6 & 2 \\10 & 1 & -1\\5 & 3 & -2\end{array}\right|}{-14}=\frac{(2+30+60)-(10+120+3)}{-14}=\frac{92-133}{-14}=\frac{-41}{-14}=\frac{41}{14}$$

$$y=\frac{\left|\begin{array}{ccc}8 & -1 & 2 \\3 & 10 & -1\\-1 & 5 & -2\end{array}\right|}{-14}=\frac{(-160-1+30)-(-20+6-40)}{-14}=\frac{-131+54}{-14}=\frac{-77}{-14}=\frac{11}{2}$$

$$z=\frac{\left|\begin{array}{ccc}8 & -6 & -1 \\3 & 1 & 10\\-1 & 3 & 5\end{array}\right|}{-14}=\frac{(40+60-9)-(1-90+240)}{-14}=\frac{91-151}{-14}=\frac{-60}{-14}=\frac{30}{7}$$

Ejemplo 2

La regla de Cramer también es útil cuando el sistema es compatible indeterminado. Consideremos el sistema siguiente:

$$\begin{cases}x+y+z+t=4\\x-y+z=1\\y-z+t=1\end{cases}$$

La matriz de los coeficientes es

$$A=\left(\begin{array}{cccc}1 & 1 & 1 & 1 \\1 & -1 & 1 & 0 \\0 & 1 & -1 & 1 \end{array}\right)$$

cuyo rango es 3 porque contienen un menor de orden tres distinto de cero:

$$\left|\begin{array}{ccc}1 & 1 & 1 \\1 & -1 & 1 \\0 & 1 & -1\end{array}\right|=(1+1)-(-1+1)=2-0=2$$

Por tanto, el rango de la matriz ampliada también es 3 (el menor anterior nos serviría para demostrarlo) y, como el número de incógnitas es 4, el sistema es compatible determinado. El grado de libertad del sistema es igual al número de incógnitas menos el rango, en este caso, es igual a 1. Si llamamos \(t=\lambda\) el sistema lo podemos reescribir así:

\begin{cases}x+y+z=4-\lambda\\x-y+z=1\\y-z=1-\lambda\end{cases}

El determinante hallado anteriormente es el determinante de la matriz de los coeficientes de este sistema, es decir, \(|A|=2\). Aplicando la regla de Cramer tenemos:

$$x=\frac{\left|\begin{array}{ccc}4-\lambda & 1 & 1 \\1 & -1 & 1\\1-\lambda & 1 & -1 \end{array}\right|}{2}=\frac{(4-\lambda+1-\lambda+1)-(-1+\lambda-1+4-\lambda)}{2}=\frac{4-2\lambda}{2}=2-\lambda$$

$$y=\frac{\left|\begin{array}{ccc}1 & 4-\lambda & 1 \\1 & 1 & 1\\0 & 1-\lambda & -1\end{array}\right|}{2}=\frac{(-1+1+\lambda)-(-4+\lambda+1-\lambda)}{2}=\frac{3-\lambda}{2}$$

$$z=\frac{\left|\begin{array}{ccc}1 & 1 & 4-\lambda \\1 & -1 & 1\\0 & 1 & 1-\lambda \end{array}\right|}{2}=\frac{(-1+\lambda+4-\lambda)-(1-\lambda+1)}{2}=\frac{1+\lambda}{2}$$

Por tanto, las soluciones son:

$$(x,y,z,t)=\left(2-\lambda,\frac{3-\lambda}{2},\frac{1+\lambda}{2},\lambda\right)$$

Soluciones que también podemos escribir del siguiente modo:

$$(x,y,z,t)=\left(2,\frac{3}{2},\frac{1}{2},0\right)+\lambda\left(-1,-\frac{1}{2},\frac{1}{2},1\right)$$

Desde el punto de vista geométrico, la igualdad anterior viene ser la ecuación vectorial de una recta en un espacio de dimensión cuatro. O sea, que el sistema de ecuaciones del cual hemos extraído las soluciones no es otra cosa que una recta en el hiperespacio.

Ejemplo 3

Usando la regla de Cramer también podemos hallar el punto de corte de dos rectas. Por ejemplo, sean las rectas

$$r\equiv\begin{cases}x+2y-z=1\\-x+y-3z=2\end{cases}\quad;\quad s\equiv\begin{cases}x+y=0\\3x+2y+z=a\end{cases}$$

Vamos a hallar el valor del parámetro \(a\) para el que ambas rectas son secantes y, para ese valor de \(a\), hallaremos el punto de corte. El sistema de ecuaciones formado por ambas rectas es

$$\begin{cases}x+2y-z=1\\-x+y-3z=2\\x+y=0\\3x+2y+z=a\end{cases}$$

La matriz de los coeficientes es

$$A=\left(\begin{array}{ccc}1 & 2 & -1 \\-1 & 1 & -3 \\1 & 1 & 0 \\3 & 2 & 1 \end{array}\right)$$

cuyo rango es 3 ya que contiene un menor de orden tres distinto de cero, por ejemplo

$$\left|\begin{array}{ccc}1 & 2 & -1 \\ -1 & 1 & -3 \\1 & 1 & 0\end{array}\right|=(-6+1)-(-1-3)=-5+4=-1\neq0$$

La matriz ampliada \(A|b\) es una matriz cuadrada de orden 4. Hallemos su determinante:

$$\left|\begin{array}{cccc}1 & 2 & -1 & 1 \\-1 & 1 & -3 & 2 \\1 & 1 & 0 & 0 \\3 & 2 & 1 & a\end{array}\right|=\left|\begin{array}{cccc}1 & 1 & -1 & 1 \\-1 & 2 & -3 & 2 \\1 & 0 & 0 & 0 \\3 & -1 & 1 & a\end{array}\right|=\left|\begin{array}{ccc}1 & -1 & 1 \\2 & -3 & 2 \\ -1 & 1 & a\end{array}\right|=\left|\begin{array}{ccc}1 & -1 & 1 \\0 & -1 & 0 \\0 & 0 & a+1 \end{array}\right|=-a-1$$

En el primer paso se ha restado a la segunda columna la primera. Luego se ha desarrollado por la tercera fila.

De lo anterior se deduce que si \(a\neq-1\), el determinante anterior es distinto de cero, o lo que es lo mismo, el rango de la matriz ampliada es \(4\). Y como el rango de la matriz de los coeficientes es \(3\), el sistema será incompatible. En este caso las rectas no serán secantes (serán paralelas o se cruzarán).

Sin embargo, si \(a=-1\), el determinante anterior es igual a cero, con lo que el rango de la matriz ampliada y el de la matriz de los coeficientes es tres, igual que el número de incógnitas. Se trata pues de un sistema compatible determinado (solución única). Es decir, ambas rectas se cortan en un punto. Para hallar el punto de corte resolvemos el sistema. Como el rango es tres, podemos eliminar una de las ecuaciones y usar la regla de Cramer. Es decir, resolveremos el sistema siguiente:

$$\begin{cases}x+2y-z=1\\-x+y-3z=2\\x+y=0\\ \end{cases}$$

Ya hemos visto que el determinante de la matriz de los coeficientes es igual a \(-1\). Por tanto, por la regla de Cramer:

$$x=\frac{\left|\begin{array}{ccc}1 & 2 & -1 \\2 & 1 & -3 \\0 & 1 & 0\end{array}\right|}{-1}=\frac{(-2)-(-3)}{-1}=\frac{1}{-1}=-1$$

$$y=\frac{\left|\begin{array}{ccc}1 & 1 & -1 \\-1 & 2 & -3 \\1 & 0 & 0\end{array}\right|}{-1}=\frac{(-3)-(-2)}{-1}=\frac{-1}{-1}=1$$

$$z=\frac{\left|\begin{array}{ccc}1 & 2 & 1 \\-1 & 1 & 2 \\1 & 1 & 0\end{array}\right|}{-1}=\frac{(4-1)-(1+2)}{-1}=\frac{0}{-1}=0$$

Resumiendo, si \(a=1\), las rectas son secantes y el punto de corte de las rectas \(r\) y \(s\) es el punto \((-1,1,0)\).

---

Puedes ver y descargar el artículo en formato pdf aquí.

La belleza, como el dolor, hace sufrir

Thomas Mann

---

Un sistema de dos ecuaciones lineales de primer grado con tres incógnitas tiene la siguiente forma

$$\left\{ \begin{array}{l}Ax + By + Cz + D = 0\\A’x + B’y + C’z + D = 0\end{array} \right.\qquad(1)$$

Ya sabemos que una ecuación lineal de primer grado con tres incógnitas es, desde el punto de vista geométrico, un plano en el espacio. En este caso tenemos dos en su forma general:

$$\pi \equiv Ax + By + Cz + D = 0\quad \text{;}\quad \pi’ \equiv A’x + B’y + C’z + D’ = 0$$

Las posibles posiciones relativas de dos planos en el espacio son tres: coincidentes, paralelos y secantes. Utilizaremos el teorema de Rouché para interpretar las soluciones del sistema e identificarlas con la posición relativa correspondiente.

Sean pues, respectivamente,

$$\left( {\begin{array}{*{20}{c}}A&B&C\\{A’}&{B’}&{C’}\end{array}} \right)\quad\text{;}\quad\left( {\begin{array}{*{20}{c}}A&B&C&-D\\{A’}&{B’}&{C’}&{-D’}\end{array}} \right)$$

la matriz de los coeficientes y la matriz ampliada del sistema $(1)$. Como hay tres incógnitas escribiremos \(n=3\). Veamos ahora los casos que se pueden presentar.

Caso 1

$${\rm{rango}}\left( {\begin{array}{*{20}{c}}A&B&C\\{A’}&{B’}&{C’}\end{array}} \right) = {\rm{rango}}\left( {\begin{array}{*{20}{c}}A&B&C&{-D}\\{A’}&{B’}&{C’}&{-D’}\end{array}} \right) = 1 < 3 = n$$

El sistema es compatible indeterminado. Es decir, existen infinitas soluciones. En este caso las filas son proporcionales, con lo que los dos planos serán coincidentes. La condición pues para que esto ocurra es

$$\pi \equiv \pi’ \Leftrightarrow \frac{A}{{A’}} = \frac{B}{{B’}} = \frac{C}{{C’}} = \frac{D}{{D’}}$$

Caso 2

$${\rm{rango}}\left( {\begin{array}{*{20}{c}}A&B&C\\{A’}&{B’}&{C’}\end{array}} \right) = 1 \ne {\rm{rango}}\left( {\begin{array}{*{20}{c}}A&B&C&{-D}\\{A’}&{B’}&{C’}&{-D’}\end{array}} \right) = 2$$

El sistema no tiene solución, con lo que los planos serán paralelos. En este caso las filas de la matriz de los coeficientes son proporcionales, pero no lo son las de la matriz ampliada. Por tanto es fácil deducir que la condición para que los dos planos sean paralelos es la siguiente:

$$\pi\, |\,|\,\pi’ \Leftrightarrow \frac{A}{{A’}} = \frac{B}{{B’}} = \frac{C}{{C’}} \ne \frac{D}{{D’}}$$

Caso 3

$${\rm{rango}}\left( {\begin{array}{*{20}{c}}A&B&C\\{A’}&{B’}&{C’}\end{array}} \right) = {\rm{rango}}\left( {\begin{array}{*{20}{c}}A&B&C&{-D}\\{A’}&{B’}&{C’}&{-D’}\end{array}} \right) = 2 < 3 = n$$

El sistema vuelve a ser compatible indeterminado. Es decir, hay infinitas soluciones. La única posibilidad es que estas soluciones, al ser el rango dos y no ser las filas proporcionales, estén sobre la recta donde se cortan ambos planos. En este caso los planos son secantes según una recta: \(\pi \cap \pi’ = r\). Las soluciones, o lo que es lo mismo, la recta de corte de ambos planos, se puede obtener hallando las soluciones del sistema (que dependerán de un parámetro). De este modo obtendríamos las ecuaciones paramétricas de la recta. De hecho, si los planos son secantes según una recta \(r\), al conjunto de las dos ecuaciones del sistema se les llama ecuaciones implícitas de la recta:

$$r \equiv \left\{ \begin{array}{l}Ax + By + Cz + D = 0\\A’x + B’y + C’z + D = 0\end{array} \right.$$

Veamos un ejemplo de este último caso.

Sean los planos \(\pi \equiv 2x – 3y + z – 1 = 0\) y \(\pi’ \equiv – x + y – 4z + 1 = 0\). El sistema formado por ambos es:

$$\left\{ \begin{array}{l}2x-3y + z-1 = 0\\-x + y-4z + 1 = 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}2x-3y + z = 1\\-x + y-4z =-1\end{array} \right.$$

Es muy fácil darse cuenta de que

$${\rm{rango}}\left( {\begin{array}{*{20}{c}}2&{-3}&1\\{-1}&1&{-4}\end{array}} \right) = {\rm{rango}}\left( {\begin{array}{*{20}{c}}2&{-3}&1&1\\{-1}&1&{-4}&{-1}\end{array}} \right) = 2$$

pues hay un menor de orden dos distinto de cero:

$$\left| {\begin{array}{*{20}{c}}2&{-3}\\{-1}&1\end{array}} \right| = 2-3 =-1 \ne 0$$

Si llamamos \(z=\lambda\), el sistema lo podemos escribir así:

$$\left\{ \begin{array}{l}2x-3y = 1-\lambda \\-x + y =-1 + 4\lambda\end{array} \right.$$

cuyas soluciones son, aplicando la regla de Cramer:

$$x = \frac{{\left| {\begin{array}{*{20}{c}}{1-\lambda }&{ – 3}\\{-1 + 4\lambda }&1\end{array}} \right|}}{{-1}} = \frac{{1-\lambda-\left( {3-12\lambda } \right)}}{{-1}} = \frac{{-2 + 11\lambda }}{{-1}} = 2-11\lambda$$

$$y = \frac{{\left| {\begin{array}{*{20}{c}}2&{1-\lambda }\\{-1}&{-1 + 4\lambda }\end{array}} \right|}}{{-1}} = \frac{{-2 + 8\lambda-\left( {-1 + \lambda } \right)}}{{-1}} = \frac{{-1 + 7\lambda }}{{-1}} = 1-7\lambda$$

Estas soluciones las podemos escribir así:

$$\left( {x,y,z} \right) = \left( {2-11\lambda ,1-7\lambda ,\lambda } \right) = \left( {2,1,0} \right) + \lambda \left( {-11,7,1} \right)$$

que no es otra cosa que la ecuación vectorial de la recta que pasa por el punto \(P\left( {2,1,0} \right)\) y tiene vector director \(\vec u = \left( {-11,-7,1} \right)\).

En la siguiente figura se pueden apreciar los dos planos y la recta donde se cortan ambos.

---

Puedes ver y descargar el artículo en formato pdf aquí.

Mejor que de nuestro juicio, debemos fiarnos del cálculo algebraico

Leonhard Euler

---

En un artículo anterior habíamos hablado sobre la ecuación lineal de primer grado con dos incógnitas y sobre la recta en el plano afín.

Esas ideas se pueden extender al espacio en tres dimensiones. Así que vamos allá.

Ya sabemos que una ecuación lineal es una ecuación polinómica de grado uno con una o varias incógnitas.

Si la ecuación tiene tres incógnitas la ecuación adopta la forma

$$ax+by+cz+d=0$$

donde \(a\), \(b\), \(c\) y \(d\) son números reales, y las incógnitas son \(x\), \(y\), \(z\). Llamando, por ejemplo, \(x=\lambda\), \(y=\mu\), podemos despejar la incógnita \(z\):

$$ax + by + cz + d = 0 \Rightarrow cz =-a\lambda-b\mu-d\Rightarrow z =-\frac{a}{c}\lambda-\frac{b}{c}\mu-\frac{d}{c}$$

El hecho de llamar \(\lambda\) a la incógnita \(x\) y \(\mu\) a la incógnita \(y\), viene a decir que las incógnitas \(x\) e \(y\) pueden tomar cualquier valor real, a los que llamaremos parámetros. Por tanto, la incógnita \(z\) depende del valor que le demos a los parámetros \(\lambda\) y \(\mu\).

Podemos escribir las soluciones en forma de terna ordenada, de la siguiente manera:

$$\left( {x,y,z} \right) = \left( {\lambda\, ,\mu\, ,-\frac{a}{c}\lambda-\frac{b}{c}\mu-\frac{d}{c}} \right)$$

Por ejemplo, sea la ecuación lineal de primer grado con tres incógnitas \(x-2y+3z-5=0\). En este caso \(a=1\), \(b=-2\), \(c=3\) y \(d=-5\). Por tanto, las soluciones son de la forma

$$\left( {x,y,z} \right) = \left( {\lambda\, ,\mu\, ,-\frac{1}{3}\lambda-\frac{{-2}}{3}\mu-\frac{{-5}}{3}} \right) = \left( {\lambda\, ,\mu\, ,-\frac{1}{3}\lambda + \frac{2}{3}\mu + \frac{5}{3}} \right)$$

Ahora, si damos valores a \(\lambda\) y a \(\mu\) podemos ir obteniendo los valores de \(z\). Por ejemplo, si \(\lambda=5\) y \(\mu=0\), entonces

$$z = -\frac{1}{3}\lambda + \frac{2}{3}\mu + \frac{5}{3} = -\frac{1}{3} \cdot 5 + \frac{2}{3} \cdot 0 + \frac{5}{3} = -\frac{5}{3} + \frac{5}{3} = 0$$

Procediendo de manera similar podemos obtener las ternas de soluciones siguientes:

$$\lambda=0\ ,\ \mu=0\Rightarrow \left( {x,y,z} \right) = \left( {0,0,\frac{5}{3}} \right)$$

$$\lambda=0\ ,\ \mu=-\frac{5}{2}\Rightarrow \left( {x,y,z} \right) = \left( {0,-\frac{5}{2},0} \right)$$

$$\lambda=2\ ,\ \mu=2\Rightarrow \left( {x,y,z} \right) = \left( {2,2,\frac{7}{3}} \right)$$

$$\lambda=-3\ ,\ \mu=-1\Rightarrow \left( {x,y,z} \right) = \left( {-3,-1,-2} \right)$$

Podemos representar incluso los valores anteriores usando unos ejes de coordenadas, es decir, fijando un sistema de referencia afín tridimensional (el espacio afín). Este sistema es el habitual, es decir, \(R = \left\{ {O,\,\,\left\{ {{\rm{i}},{\rm{j}},{\rm{k}}} \right\}} \right\}\), donde \({\rm{i}} = \left( {1,0,0} \right)\), \({\rm{j}} = \left( {0,1,0} \right)\), \({\rm{k}} = \left( {0,0,1} \right)\) (ya se habló sobre este sistema de referencia en un artículo anterior, dedicado a los sistemas de dos ecuaciones lineales de primer grado con dos incógnitas). Pues bien, todas las ternas que son soluciones de la ecuación \(x-2y+3z-5=0\) están situadas en un mismo plano \(\pi\), con lo que llamaremos

$$\pi\equiv x-2y+3z-5=0$$

Lo podemos apreciar en la figura siguiente, en la que incluso se observa el punto del plano \(\left( { – 3, – 1,2} \right)\), que también representa al vector de las mismas coordenadas.

Las soluciones de una ecuación lineal de primer grado con tres incógnitas, \(ax + by + cz + d = 0\), también las podemos escribir así:

$$\left( {x,y,z} \right) = \left( {\lambda\, ,\mu\, , -\frac{a}{c}\lambda-\frac{b}{c}\mu-\frac{d}{c}} \right) = \left( {\lambda ,0,-\frac{a}{c}\lambda } \right) + \left( {0,\mu ,-\frac{b}{c}\mu } \right) + \left( {0,0,-\frac{d}{c}} \right) \Rightarrow$$

$$\Rightarrow \left( {x,y,z} \right) = \lambda \left( {1,0,-\frac{a}{c}} \right) + \mu \left( {0,1,-\frac{b}{c}} \right) + \left( {0,0,-\frac{d}{c}} \right)$$

Siguiendo con el ejemplo anterior podemos escribir las soluciones de la ecuación $x-2y+3z-5=0$ del siguiente modo:

$$\left( {x,y,z} \right) = \lambda \left( {1,0,-\frac{1}{3}} \right) + \mu \left( {0,1,\frac{2}{3}} \right) + \left( {0,0,\frac{5}{3}} \right)$$

Geométricamente, la expresión anterior indica que el plano \(\pi\equiv x-2y+3z-5=0\) es el plano paralelo al plano que contiene a los vectores \(\left( {1,0,-\dfrac{1}{3}} \right)\), \(\left( {0,1,\dfrac{2}{3}} \right)\) y que pasa por el punto \(\left( {0,0,\dfrac{5}{3}} \right)\). Dicho de otro modo: todos los puntos de este plano son los extremos de los vectores que se obtienen al sumar cualquier vector proporcional al vector \(\left( {1,0,-\dfrac{1}{3}} \right)\) con cualquier vector proporcional al vector \(\left( {0,1,\dfrac{2}{3}} \right)\), y con el vector \(\left( {0,0,\dfrac{5}{3}} \right)\).

De hecho, si tomamos \(\lambda=1\) y \(\mu=1\), tenemos que un punto del plano es

$$\left( {x,y,z} \right) = 1\left( {1,0,-\frac{1}{3}} \right) + 1\left( {0,1,\frac{2}{3}} \right) + \left( {0,0,\frac{5}{3}} \right) = \left( {1,1,2} \right)$$

No es fácil imaginar esta situación en el espacio, pero con ayuda de alguna aplicación que represente figuras en tres dimensiones podemos hacernos una idea. En este caso, como en la imagen anterior, hemos utilizado Geogebra.

En la siguiente figura se observa como nuestro plano \(\pi \equiv x – 2y + 3z – 5 = 0\), es paralelo al plano que contiene a \(\left( {1,0, – \dfrac{1}{3}} \right)\) y a \(\left( {0,1,\dfrac{2}{3}} \right)\) y además pasa por el punto \(\left( {0,0,\dfrac{5}{3}} \right)\).

Se puede apreciar con claridad que el punto \(\left( {1,1,2} \right)\), generado por las soluciones correspondientes a \(\lambda=1\) y \(\mu=1\), pertenece al plano \(\pi\).

Analizando lo anterior llegamos a una conclusión: un plano viene completamente determinado por dos vectores con distinta dirección (linealmente independientes) y un punto. O lo que es lo mismo, existe un único plano que pasa por un punto dado y en dos direcciones determinadas. A los vectores que determinan el plano se le llaman vectores de dirección o vectores directores del plano.

Generalicemos esta situación desde el punto de vista vectorial. Para ello llamaremos \(O\) al origen de coordenadas, \(A\) a un punto cualquiera del espacio, \(\overrightarrow {OA} \) al vector de posición con origen en \(O\) y extremo en \(A\), y \(\vec u\) y \(\vec v\) a dos vectores con distinta dirección. La ecuación del plano que pasa por el punto \(A\) con la dirección de los vectores \(\vec u\) y \(\vec v\) viene dada por

$$\overrightarrow {OX} = \overrightarrow {OA} \, + \lambda \vec u + \mu \vec v\,,\,\,\lambda ,\mu \in \mathbb{R}$$

donde \(\overrightarrow {OX} \) es el vector de posición con origen en \(O\) generado al dar valores a los parámetros \(\lambda\) y \(\mu\).

Hemos de insistir en que las coordenadas de los vectores están escritas en base al sistema de referencia \(R = \left\{ {O,\,\,\left\{ {{\rm{i}},{\rm{j}},{\rm{k}}} \right\}} \right\}\) del que hemos hablado anteriormente. Es decir, hemos instalado en el espacio unos ejes de coordenadas: el eje \(X\) para la anchura, el eje \(Y\) para la profundidad, y el eje \(Z\) para la altura. Así, cuando hablamos de tomar el vector \(\vec e = \left( {1,1,2} \right)\) , y lo visualizamos en el espacio como un segmento orientado desde el origen de coordenadas \(O = \left( {0,0,0} \right)\) hasta el extremo en el punto de coordenadas \(\left( {1,1,2} \right)\), lo que estamos haciendo realmente es la siguiente operación:

$$\left( {1,1,2} \right) = 1\left( {1,0,0} \right) + 1\left( {0,1,0} \right) + 2\left( {0,0,1} \right) = 1 \cdot {\rm{i}} + 1 \cdot {\rm{j}} + 2 \cdot {\rm{k}}$$

O lo que es lo mismo, el vector \(\vec e = \left( {1,1,2} \right)\) es aquel que tiene una unidad de anchura, otra de profundad y dos unidades de altura.

Los vectores \({\rm{i}} = \left( {1,0,0} \right)\), \({\rm{j}} = \left( {0,1,0} \right)\), \({\rm{k}} = \left( {0,0,1} \right)\) situados sobre el eje \(X\), sobre el eje \(Y\) y sobre el eje \(Z\), tienen módulo \(1\) y son perpendiculares. Se dice que los tres vectores son ortonormales o que forman una base ortonormal del espacio. Además cualquier vector \(\left( {a,b,c} \right)\) lo podemos escribir así:

$$\left( {a,b,c} \right) = a\left( {1,0,0} \right) + b\left( {0,1,0} \right) + c\left( {0,0,1} \right) = a \cdot {\rm{i}} + b \cdot {\rm{j}} + c \cdot {\rm{k}}$$

La igualdad anterior expresa que todo vector del espacio, o lo que es lo mismo, todo el espacio, se puede generar a partir de los vectores \({\rm{i}} = \left( {1,0,0} \right)\), \({\rm{j}} = \left( {0,1,0} \right)\), \({\rm{k}} = \left( {0,0,1} \right)\). Se dice que todo vector del espacio es una combinación lineal de \({\rm{i}} = \left( {1,0,0} \right)\), \({\rm{j}} = \left( {0,1,0} \right)\), \({\rm{k}} = \left( {0,0,1} \right)\). Estos vectores, junto con el origen de coordenadas \(O\) forman el sistema de referencia ortonormal \(R = \left\{ {O,\,\,\left\{ {{\rm{i}},{\rm{j}},{\rm{k}}} \right\}} \right\}\).

La geometría en el espacio afín empieza de este modo. Se considera un sistema de referencia afín ortonormal \(R = \left\{ {O,\,\,\left\{ {{\rm{i}},{\rm{j}},{\rm{k}}} \right\}} \right\}\). Se sabe que todo vector que se apoye en \(O\) se puede poner como combinación lineal de \({\rm{i}}\), de \({\rm{j}}\) y de \({\rm{k}}\):

$$X = \overrightarrow {OX} = {x_1}{\rm{i}} + {x_2}{\rm{j}} + {x_3}{\rm{k}} = \left( {{x_1},{x_2},{x_3}} \right)$$

Por tanto, un vector cualquiera del espacio lo podemos «atrapar» en nuestro sistema de referencia. Todo vector \(\vec e\) del espacio tiene un origen \(A\left( {{a_1},{a_2},{a_3}} \right)\) y un extremo \(B\left( {{b_1},{b_2},{b_3}} \right)\), y por tanto \(\vec e = \overrightarrow {AB}\). Además:

$$\overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {AB} \Rightarrow \overrightarrow {AB} = \overrightarrow {OB}-\overrightarrow {OA} \Rightarrow$$

$$\Rightarrow \overrightarrow {AB} = \left( {{b_1},{b_2},{b_3}} \right)-\left( {{a_1},{a_2},{a_3}} \right) \Rightarrow \overrightarrow {AB} = \left( {{b_1}-{a_1},{b_2}-{a_2},{b_3}-{a_3}} \right)$$

Por ejemplo, el vector \(\vec e\) que une el punto \(P\left( {3,-1,2} \right)\) con el punto \(Q\left( {2,-\,3,-1} \right)\) es

$$\vec e = \overrightarrow {PQ} = \left( {2-3,-3-\left( {-1} \right),-1-2} \right) = \left( {-1,-2,-3} \right)$$

Nuestro vector \(\vec e\) acaba de ser escrito en base a nuestro sistema de referencia. Hay infinitos vectores en el espacio con el mismo módulo, dirección y sentido, pero sólo uno que se apoya en el origen \(O\) de nuestro sistema de referencia. Al conjunto de todos los vectores con el mismo módulo, dirección y sentido se le llama vector libre del espacio.

Con las consideraciones anteriores la ecuación vectorial del plano que pasa por el punto \(A\) con la dirección de los vectores \(\vec u\) y \(\vec v\), \(\overrightarrow {OX} = \overrightarrow {OA} \, + \lambda \vec u + \mu \vec v\,,\,\,\lambda ,\,\,\mu \in \mathbb{R}\), adquiere todo su sentido.

Si la ecuación vectorial la expresamos en coordenadas tenemos:

$$\left( {x,y,z} \right) = \left( {{a_1},{a_2},{a_3}} \right) + \lambda \left( {{u_1},{u_2},{u_3}} \right) + \mu \left( {{v_1},{v_2},{v_3}} \right) \Rightarrow$$

$$\Rightarrow \left( {x,y,z} \right) = \left( {{a_1} + \lambda {u_1} + \mu {v_1},{a_2} + \lambda {u_2} + \mu {v_2},{a_3} + \lambda {u_3} + \mu {v_3}} \right)$$

Igualando coordenadas:

$$\left\{ \begin{array}{l} x = {a_1} + \lambda {u_1} + \mu {v_1}\\ y = {a_2} + \lambda {u_2} + \mu {v_2}\\ z = {a_3} + \lambda {u_3} + \mu {v_3} \end{array} \right.$$

Las ecuaciones anteriores reciben el nombre de ecuaciones paramétricas del plano. Estas ecuaciones las podemos ver como un sistema de tres ecuaciones con dos incógnitas: \(\lambda\) y \(\mu\).

$$\left\{ \begin{array}{l} \lambda {u_1} + \mu {v_1} = x-{a_1}\\ \lambda {u_2} + \mu {v_2} = y-{a_2}\\ \lambda {u_3} + \mu {v_3} = z-{a_3} \end{array} \right.$$

Si de este sistema eliminamos los parámetros \(\lambda\) y \(\mu\) obtenemos la ecuación general o implícita del plano, que será una ecuación lineal de primer grado con tres incógnitas:

$$Ax+By+Cz+D=0$$

Veamos con un ejemplo cómo eliminar los parámetros. Supongamos que queremos hallar la ecuación general del plano que pasa por el punto \(A\left( {2,3,5} \right)\) y es paralelo a los vectores \(\vec u = \left( { – 1, – 2, – 3} \right)\), \(\vec v = \left( {1,3,5} \right)\). Sus ecuaciones paramétricas serán:

$$\left\{ \begin{array}{l} x = 2-\lambda+\mu \\ y = 3-2\lambda+3\mu \\ z = 5-3\lambda + 5\mu \end{array} \right.$$

Y de aquí:

$$\left\{ \begin{array}{l}-\lambda+\mu = x-2\\ -2\lambda+3\mu = y-3\\ -3\lambda + 5\mu = z-5 \end{array} \right.$$

Consideremos que las incógnitas son \(\lambda\) y \(\mu\) y apliquemos el método de Gauss para resolver el sistema:

$$\left( {\begin{array}{*{20}{c}} {-1}&1&{x-2}\\{-2}&3&{y-3}\\{-3}&5&{z-5}\end{array}} \right)\longrightarrow\left( {\begin{array}{*{20}{c}}{-1}&1&{x-2}\\ 0&1&{y-2x+1}\\0&2&{z-3x + 1}\end{array}} \right)\longrightarrow\left( {\begin{array}{*{20}{c}}{-1}&1&{x-2}\\0&1&{y-2x + 1}\\0&0&{x-2y + z-1}\end{array}} \right)$$

De lo anterior se deduce, para que el sistema tenga soluciones (precisamente las soluciones son todos los puntos del plano), que \(x-2y + z-1 = 0\), justamente la ecuación general o implícita del plano.

Sin hacer el último paso en el método de Gauss también se obtiene lo mismo. Las dos últimas ecuaciones asociadas son

$$\left\{ \begin{array}{l}\mu = y-2x + 1\\2\mu = z-3x + 1\end{array} \right.$$

y de aquí se obtiene, por igualación, que

$$y-2x + 1 = \frac{{z-3x + 1}}{2} \Rightarrow 2y-4x+2=z-3x+1 \Rightarrow x-2y+z-1=0$$

---

Puedes ver y descargar el artículo en formato pdf aquí.

El que tiene fe en sí mismo no necesita que los demás crean en él

Miguel de Unamuno

---

Un sistema de dos ecuaciones lineales de primer grado con dos incógnitas lo podemos escribir de la siguiente manera:

$$\left\{ \begin{array}{l}Ax + By + C = 0\\A’x + B\,’y + C’ = 0\end{array} \right.\quad\textbf{(1)}$$

Ya sabemos que una ecuación lineal de primer grado con dos incógnitas es, desde el punto de vista geométrico, una recta en el plano. En este caso tenemos dos en su forma general:

$$r \equiv Ax + By + C = 0\quad\text{;}\quad s\equiv A’x + B\,’y + C’ = 0$$

Las posibles posiciones relativas de dos rectas en el plano son tres: coincidentes, paralelas y secantes.

Si son coincidentes es porque una recta es la misma que la otra salvo un factor numérico, es decir,

$$Ax + By + C = k\left( {A’x + B\,’y + C’} \right) = 0 \Rightarrow$$

$$\Rightarrow Ax + By + C = kA’x + kB\,’y + kC’ = 0\,\,,\,\,k \in \mathbb{R}$$

De aquí se deduce que \(A = kA’\,,\,B = kB\,’\,,\,C = kC’\) y despejando \(k\) obtenemos una condición para que las dos rectas coincidan:

$$r \equiv s \Leftrightarrow \frac{A}{{A’}} = \frac{B}{{B\,’}} = \frac{C}{{C’}}$$

En este caso el sistema \(\textbf{(1)}\) tiene infinitas soluciones pues las dos rectas, al ser coincidentes, tienen en común todos sus puntos.

Si las dos rectas son paralelas tienen la misma dirección, los vectores directores de \(r\) y \(s\) son iguales o proporcionales. Es decir, llamando \(\vec u\) al vector director de \(r\), y \(\vec v\) al vector director de \(s\), tenemos que \(\vec u = k\vec v\), donde \(k\) es un número real. Pero recordemos que los vectores directores se podían obtener fácilmente de la ecuación general de la recta: \(\vec u = \left( {-B,A} \right)\) y \(\vec v = \left( {-B\,’,A’} \right)\), con lo que:

$$\vec u = k\vec v \Leftrightarrow \left( {-B,A} \right) = k\left( {-B\,’,A’} \right) \Leftrightarrow \left( { – B,A} \right) = \left( { – kB\,’,kA’} \right) \Leftrightarrow$$

$$\Leftrightarrow \left\{ \begin{array}{l}-B=-kB\,’\\A = kA’\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \frac{B}{{B\,’}}\\k = \frac{A}{{A’}}\end{array} \right. \Leftrightarrow \frac{A}{{A’}} = \frac{B}{{B\,’}}$$

Así pues para que dos rectas sean paralelas tenemos la siguiente condición:

$$r\,|\,|\,s \Leftrightarrow \frac{A}{{A’}} = \frac{B}{{B\,’}} \ne \frac{C}{{C’}}$$

En este caso el sistema \(\textbf{(1)}\) no tienen ninguna solución (esto es obvio: dos rectas paralelas no tienen ningún punto en común, no se cortan en ningún punto).

Por último, si las dos rectas son secantes, han de tener distinta dirección, con lo que sus vectores directores no serán proporcionales. Esto nos lleva a la siguiente condición:

$$r \cap s = \left\{ P \right\} \Leftrightarrow \frac{A}{{A’}} \ne \frac{B}{{B\,’}}$$

En este caso el sistema \(\textbf{(1)}\) tienen una única solución. Esta solución es el punto de corte de las rectas \(r\) y \(s\): \(P\left( {a,b} \right)\).

Lo veremos un ejemplo. Consideremos el sistema de ecuaciones

$$\displaystyle\left\{ \begin{array}{l}2x-3y-8 = 0\\-5x-y + 3 = 0\end{array} \right.$$

Este sistema está; formado por las rectas \(r \equiv 2x-3y-7 = 0\) y \(s \equiv -5x-y + 3 = 0\).

Como tenemos que \(\dfrac{2}{{-5}} \ne \dfrac{{-3}}{{-1}}\), entonces las rectas son secantes. Si queremos saber el punto de corte basta resolver el sistema. Por reducción es muy sencillo. Multiplicando la segunda ecuación por \(-3\) tenemos:

$$\displaystyle\left\{ \begin{array}{l}2x-3y-8 = 0\\15x + 3y-9 = 0\end{array} \right.$$

Ahora, si a la segunda ecuación se le suma la primera el sistema queda reducido al este otro:

$$\displaystyle\left\{ \begin{array}{l}2x-3y-8 = 0\\17x-17 = 0\end{array} \right.$$

Despejando $x$ de la segunda ecuación: \(17x-17 = 0 \Rightarrow x = 1\). Y sustituyendo este valor en la primera ecuación despejaremos el valor de \(y\): \(2-3y-8 = 0 \Rightarrow -3y-6 = 0 \Rightarrow y =-2\).

Este método de reducción es un caso particular de otro más general, conocido como método de Gauss para la resolución de sistemas de ecuaciones lineales.

La interpretación geométrica es muy sencilla: el punto de corte de las rectas $r\equiv2x-3y-8=0$ y $s\equiv-5x-y+3=0$ es \(P\left( {1, – 2} \right)\). Esto se escribe simbólicamente así:

$$r\cap s=P(-1,2)$$

Se puede apreciar en la siguiente figura.

Puede que ahora sea un buen momento de hablar de independencia lineal. Es un concepto muy sencillo. Para ello vamos a pensar en dimensión tres, en un espacio tridimensional como en el que vivimos. Es decir, vamos a fijar un sistema de referencia afín donde cada punto y cada vector tiene tres coordenadas. Este sistema de referencia afín lo podemos escribir as&iacute;: \(R = \left\{ {O\,,\,\left\{ {{\rm{i}},{\rm{j}},{\rm{k}}} \right\}} \right\}\) donde \({\rm{i}} = \left( {1,0,0} \right)\), \({\rm{j}} = \left( {0,1,0} \right)\) y \({\rm{k}} = \left( {0,0,1} \right)\). Algo así como decir que \(\text{i}\) mide la anchura, \(\text{j}\) la profundidad y \(\text{k}\) la altura. De modo que, por ejemplo, el vector \(\vec u\left( {3,4,2} \right)\) tiene tres unidades de anchura, cuatro de profundidad y dos de altura.

Pues bien, un vector es siempre linealmente independiente y genera una recta (la recta que lo contiene, que es un espacio de dimensión uno). Dos vectores son linealmente independientes si tienen distinta dirección, en cuyo caso generan todo un plano (el plano que los contiene, que es de dimensión dos). Si dos vectores no tienen distinta dirección serán proporcionales (uno se puede poner como el otro multiplicado por un número) y no son linealmente independientes. Tres vectores son linealmente independientes si no están situados en un mismo plano (no coplanarios) y generan todo el espacio, que es de dimensón tres.

¿Qué queremos decir cuando hablamos de que dos vectores linealmente independientes generan el plano que los contiene? Pues que, combinando adecuadamente los dos vectores, podemos llegar a cualquier otro vector del plano.

Veamos un ejemplo. Para ello volvamos a la dimensión dos. Consideremos los vectores \(\left( {1,3} \right)\) y \(\left( {-2,1} \right)\), que tienen distinta dirección. Por tanto, según hemos definido anteriormente, son linealmente independientes, y generan todo el plano de dimensión dos. Esto quiere decir que cualquier otro vector se puede poner como combinación de ellos. Pensemos, por ejemplo en el vector \(\left( {3,-5} \right)\). ¿Podremos llegar a él usando los vectores \(\left( {1,3} \right)\) y \(\left( {-2,1} \right)\)? Es decir, ¿existirán números reales \(x\), \(y\) tales que \(x\left( {1,3} \right) + y\left( {-2,1} \right) = \left( {3,-5} \right)\)? Seguro que sí. Veamos:

$$x\left( {1,3} \right) + y\left( {-2,1} \right) = \left( {3,-5} \right) \Leftrightarrow \left( {x,3x} \right) + \left( {-2y,y} \right) = \left( {3,-5} \right) \Leftrightarrow$$

$$\Leftrightarrow\left( {x-2y,3x + y} \right) = \left( {3,-5} \right) \Leftrightarrow \left\{ \begin{array}{l}x-2y = 3\\3x + y =-5\end{array} \right.$$

Resolviendo el sistema anterior se obtiene \(x=-1\), \(y=-2\). Esto quiere decir que si el vector \(\left( {1,3} \right)\) lo multiplicamos por \(-1\) (o sea, le cambiamos el sentido), el vector \(\left( {-2,1} \right)\) lo multiplicamos por \(-2\) (o sea, lo duplicamos en longitud y le cambiamos el sentido) y, finalmente, sumamos ambos resultados, obtenemos como resultado el vector \(\left( {3,-5} \right)\). Esto, en matemáticas, se resume diciendo que el vector \(\left( {3,-5} \right)\) se puede poner como combinación lineal de los vectores \(\left( {1,3} \right)\) y \(\left( {-2,1} \right)\):

$$\left( {3,-5} \right) =-1\left( {1,3} \right) + \left( {-2} \right)\left( {-2,1} \right)$$

Podemos ver el resultado en la figura siguiente:

Si en el sistema

$$\left\{ \begin{array}{l}Ax + By + C = 0\\A’x + B\,’y + C’ = 0\end{array} \right.$$

escribimos los términos independientes en el segundo miembro, lo podemos reescribir así:

$$\left\{ \begin{array}{l}{a_{11}}x + {a_{12}}y = {b_1}\\{a_{21}}x + {a_{22}}y = {b_2}\end{array} \right.$$

Una vez escrito así vamos incluso a disponer de una forma más cómoda el sistema.

Llamaremos, respectivamente

$$A = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}\\{{a_{21}}}&{{a_{22}}}\end{array}} \right)\quad;\quad A|b = \left( {\begin{array}{*{20}{c}}{{a_{11}}}&{{a_{12}}}&{{b_1}}\\{{a_{21}}}&{{a_{22}}}&{{b_2}}\end{array}} \right)$$

matriz de los coeficientes y matriz ampliada del sistema. No descubrimos nada nuevo si pensamos en una matriz como una disposición de elementos en filas y en columnas. Obsérvese que al escribir la matriz ampliada \(A|b\) tenemos completamente definido el sistema sin necesidad de escribir las incógnitas. Ahora, la posición relativa de las dos rectas depende del carácter de la matriz de los coeficientes \(A\) y del de la matriz ampliada \(A|b\), en el siguiente sentido:

• Si las rectas son coincidentes, las filas de la matriz \(A\) son proporcionales y las de la matriz \(A|b\) también.
• Si las rectas son paralelas, las filas de la matriz \(A\) son proporcionales, pero no los son las de la matriz \(A|b\).
• Si las rectas son secantes, las filas de la matriz \(A\) no son proporcionales y, por tanto, tampoco lo son los de la matriz \(A|b\).

Este caráter de las matrices en matemáticas se conoce con el nombre de rango de una matriz. Hemos de observar que las filas de las matrices las podemos ver como vectores (con dos, tres, cuatro,\(\ldots\,\) coordenadas). Se define el rango de una matriz como el número de filas (vectores) linealmente independientes. Esto nos lleva a reescribir la posición relativa de dos rectas, en función de los rangos de la matriz de los coeficientes \(A\) y de la matriz ampliada \(A|b\), del siguiente modo:

• Si las rectas son coincidentes, entonces \(\text{rango}A=\text{rango}A|b=1\).
• Si las rectas son paralelas, entonces \(\text{rango}A=1\neq\text{rango}A|b=2\).
• Si las rectas son secantes, entonces \(\text{rango}A=\text{rango}A|b=2\).

Estas ideas se pueden generalizar a un sistema de \(m\) ecuaciones y \(n\) incógnitas. Según el teorema de Rouché-Frobenius, para que un sistema del tipo anterior tenga solución se ha de cumplir que el rango de la matriz de los coeficientes ha de ser igual al rango de la matriz ampliada: \(\text{rango}A=\text{rango}A|b\). Además, si este número es igual al número de incógnitas \(n\), el sistema tiene solución única (sistema compatible determinado). Sin embargo, si este número es menor que el número de incógnitas, el sistema tiene infinitas soluciones (sistema compatible indeterminado). Por último, si \(\text{rango}A\neq\text{rango}A|b\). el sistema no tiene solución (sistema incompatible).

Seguiremos dándole vueltas a todo esto en un artículo que dedicaremos a los sistemas de ecuaciones lineales de primer grado con tres incógnitas,

---

Puedes ver y descargar el artículo en formato pdf aquí.

Nada hay tan práctico como una buena teoría

Kurt Lewin

---

Una ecuación lineal es una ecuación polinómica de grado uno con una o varias incógnitas. Si la ecuación solamente tiene una incógnita la ecuación es de la forma

$$ax+b=0$$

donde \(a\) y \(b\) son números reales con \(a\neq0\), y \(x\) es la incógnita.

Como \(a\neq0\), \(a\) tiene inverso, con lo que podemos despejar la incógnita con facilidad:

$$ax + b = 0\, \Rightarrow {a^{ – 1}} \cdot \left( {ax + b} \right) = {a^{ – 1}} \cdot 0 \Rightarrow {a^{ – 1}}ax + {a^{ – 1}}b = 0 \Rightarrow$$

$$\Rightarrow x + {a^{ – 1}}b = 0 \Rightarrow x = – {a^{ – 1}}b$$

Así por ejemplo, la solución de \(3x+4=0\) es \(x = – {3^{ – 1}} \cdot 4 = – \dfrac{1}{3} \cdot 4 = – \dfrac{4}{3}\).

Si la ecuación tiene dos incógnitas la ecuación adopta la forma

$$ax+by+c=0$$

donde \(a\), \(b\) y \(c\) son números reales con \(a\neq0\) y \(b\neq0\), y las incógnitas son \(x\) e \(y\). Llamando por ejemplo \(x=\lambda\), podemos despejar la incógnita \(y\).

$$ax + by + c = 0 \Rightarrow by = -a\lambda-c \Rightarrow y=-\frac{a}{b}\lambda-\frac{c}{b}$$

El hecho de llamar \(\lambda\) a la incógnita \(x\) viene a decir que la incógnita \(x\) puede tomar cualquier valor real, al que llamaremos parámetro. Por tanto, la incógnita \(y\) depende del valor que le demos al parámetro \(\lambda\).

Podemos escribir las soluciones para \(x\) y para \(y\) en forma de par ordenado, de la siguiente manera:

$$\left( {x,y} \right) = \left( {\lambda,\, -\frac{a}{b}\lambda-\frac{c}{b}} \right)$$

Veamos un ejemplo. Sea la ecuación lineal de primer grado con dos incógnitas dada por \(2x-y+3=0\). En este caso \(a=2\), \(b=-1\) y \(c=3\). Por tanto las soluciones son de la forma:

$$\left( {x,y} \right) = \left( {\lambda,\,-\frac{2}{{ – 1}}\lambda-\frac{3}{{ – 1}}} \right) = \left( {\lambda,\,2\lambda + 3} \right)$$

Ahora, si damos valores a \(\lambda\) podemos hacer una tabla de valores:

$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|}\hline x & \lambda & -5 & -4 & -3 & -2 & -1 & 0 & 1 & 2 \\ \hline y & 2\lambda+3 & -7 & -5 & -3 & -1 & 1 & 3 & 5 & 7\\ \hline\end{array}$$

Incluso podemos representar los valores anteriores usando unos ejes de coordenadas.

No es difícil darse cuenta de que podemos colocar infinitos puntos y que todos ellos formarán una recta. Por eso, a la expresión de una ecuación lineal de primer grado con dos incógnitas, también se la conoce como ecuación general de una recta.

Además, ya sabíamos que, si de la ecuación \(ax+by+c=0\), despejamos la incógnita \(y\) tenemos otra ecuación con la forma \(y=mx+n\), llamada ecuación afín de la recta. En nuestro ejemplo la ecuación afín de la recta es \(y=2x+3\). Y en esta ecuación es donde podemos con facilidad realizar también la tabla de valores anterior con el objetivo de representar gráficamente la recta dada.

Con algo de conocimiento de geometría en el plano afín podemos hacer más cosas con la ecuación lineal de primer grado con dos incógnitas. Ya hemos visto que las soluciones las podemos escribir en forma de par ordenado:

$$\left( {x,y} \right) = \left( {\lambda,\, -\frac{a}{b}\lambda-\frac{c}{b}} \right)$$

Recordemos que, dados dos pares ordenados \(\left( {a,b} \right)\), \(\left( {c,d} \right)\), y un número real \(\lambda\), la suma de pares ordenados y el producto de un número real por un par ordenado, están definidos del siguiente modo:

$$\left( {a,b} \right) + \left( {c,d} \right) = \left( {a + c,b + d} \right)\quad\text{;}\quad\lambda \left( {a,b} \right) = \left( {\lambda a,\lambda b} \right)$$

Si se establecen unos ejes cartesianos sobre un plano, un par ordenado \(\left( {a,b} \right)\) tiene una visualización gráfica: un punto en el plano. O también: el par ordenado lo podemos ver como un vector con origen en el punto \(\left( {0,0} \right)\) (origen de coordenadas) y extremo el punto \(\left( {a,b} \right)\).

Con las ideas anteriores, las soluciones de una ecuación lineal de primer grado con dos incógnitas, \(ax+by+c=0\), las podemos escribir así:

$$\left( {x,y} \right) = \left( {\lambda , -\frac{a}{b}\lambda-\frac{c}{b}} \right) = \left( {\lambda , -\frac{a}{b}\lambda } \right) + \left( {0, -\frac{c}{b}} \right) = \lambda \left( {1, -\frac{a}{b}} \right) + \left( {0, -\frac{c}{b}} \right)$$

Siguiendo con el ejemplo visto anteriormente podemos escribir las soluciones de la ecuación \(2x-y+3=0\) del siguiente modo ($a=2$, $b=-1$, $c=-3$):

$$\left( {x,y} \right) = \lambda \left( {1,2} \right) + \left( {0,3} \right)$$

La interpretación geométrica de la expresión anterior es la siguiente: la recta \(2x-y+3=0\) es la recta paralela al vector \(\left( {1,2} \right)\) que pasa por el punto \(\left( {0,3} \right)\). Dicho de otro modo: todos los puntos de esta recta son los extremos de los vectores que se obtienen al sumar cualquier vector proporcional al vector \(\left( {1,2} \right)\) con el vector \(\left( {0,3} \right)\).

Por ejemplo, si \(\lambda=1\), entonces \(\left( {x,y} \right) = – 1\left( {1,2} \right) + \left( {0,3} \right) = \left( { – 1, – 2} \right) + \left( {0,3} \right) = \left( { – 1,1} \right)\). Véase la figura siguiente:

Analizando todo lo anterior llegamos a una conclusión: una recta viene completamente determinada por un vector y un punto. O lo que es lo mismo, existe una única recta que pasa por un punto dado y en una dirección determinada. Al vector que determina la recta se le llama vector de dirección o vector director de la recta.

Generalicemos esta situación desde el punto de vista vectorial. Para ello llamaremos \(O\), al origen de coordenadas, \(A\) a un punto cualquiera del plano, \(\overrightarrow {OA}\) al vector de posición con origen en \(O\) y extremo en \(A\) y \(\vec e\) a un vector. La ecuación de la recta que pasa por el punto \(A\) con la dirección del vector \(\vec e\) viene dada por

$$\overrightarrow {OX} = \overrightarrow {OA} \, + \lambda \vec e\,,\,\,\lambda \in \mathbb{R}$$

donde \(\overrightarrow {OX}\) es el vector de posición con origen en \(O\) generado al dar un determinado valor al parámetro \(\lambda\).

Naturalmente, las coordenadas de los vectores están escritas en base a un sistema de referencia pues, en caso contrario, no podríamos trabajar con éstas. Habitualmente, y tal y como hemos hecho en el ejemplo anterior, esto es algo a lo que estamos acostumbrados cuando instalamos en el plano unos ejes cartesianos (el eje de abscisas y el eje de ordenadas). Pero es conveniente poner énfasis en esto. Cuando hablamos de tomar, por ejemplo, el vector \(\vec e = \left( { – 2,3} \right)\), y lo visualizamos en el plano como un segmento orientado desde el origen de coordenadas \(O = \left( {0,0} \right)\) hasta el extremo en el punto de coordenadas \(\left( { – 2,3} \right)\), lo que estamos haciendo realmente es la siguiente operación:

$$\left( { – 2,3} \right) = – 2\left( {1,0} \right) + 3\left( {0,1} \right)$$

Si ahora visualizamos los vectores \(\left( {1,0} \right)\) y \(\left( {0,1} \right)\) nos daremos cuenta rápidamente de que el primero está sobre el eje \(X\), el segundo sobre el eje \(Y\) y ambos tienen longitud o módulo \(1\). Además son claramente perpendiculares. En este caso se dice que la pareja de vectores son ortonormales o que forman una base ortonormal del plano.

Pero es que cualquier vector \(\left( {a,b} \right)\) lo podemos escribir así:

$$\left( {a,b} \right) = a\left( {1,0} \right) + b\left( {0,1} \right)$$

La igualdad anterior expresa que todo vector del plano, o lo que es lo mismo, todo el plano, se puede generar a partir de los vectores \(\left( {1,0} \right)\) y \(\left( {0,1} \right)\). A veces se dice que todo vector del plano es una combinación lineal de \(\left( {1,0} \right)\) y \(\left( {0,1} \right)\). Estos dos vectores, junto con el origen de coordenadas \(O\), forman lo que se conoce como sistema de referencia afín. Además, si los dos vectores del sistema son ortonormales hablaremos de un sistema de referencia ortonormal. Suele nombrarse a los dos vectores del sistema así: $\textbf{i} = \left( {1\,\,0} \right)$, $\textbf{j} = \left( {0\,\,1} \right)$.

En realidad, la geometría en el plano afín empieza por aquí. Se considera un sistema de referencia afín ortonormal $R = \left\{ O,\,\left\{ \textbf{i},\,\textbf{j} \right\} \right\}$. Se sabe que todo vector que se apoye en \(O\) se puede poner como combinación lineal de \(\textbf{i}\) y de \(\textbf{j}\): \(X = \overrightarrow {OX} = {x_1}\textbf{i} + {x_2}\textbf{j} = \left( x_1,x_2 \right)\). Por tanto, un vector cualquiera del plano lo podemos «atrapar» en nuestro sistema de referencia. ¿Cómo? Es sencillo. Todo vector \(\vec e\) del plano tiene un origen \(A\left( {{a_1},{a_2}} \right)\) y un extremo \(B\left( {{b_1},{b_2}} \right)\) y, por tanto, \(\vec e = \overrightarrow {AB} \). Pero además es que (ver figura de más abajo):

$$\overrightarrow {OB} = \overrightarrow {OA} + \overrightarrow {AB} \Rightarrow \overrightarrow {AB} = \overrightarrow {OB}-\overrightarrow {OA} \Rightarrow$$

$$\Rightarrow \overrightarrow {AB} = \left( {{b_1},{b_2}} \right)-\left( {{a_1},{a_2}} \right) \Rightarrow \overrightarrow {AB} = \left( {{b_1}-{a_1},{b_2}-{a_2}} \right)$$

Por ejemplo, el vector \(\vec e\) que une el punto \(P\left( { – 2\,,\,1} \right)\) con el punto \(Q\left( { 1\,,\,3} \right)\) es

$$\vec e = \overrightarrow {PQ} = \left( {1-\left( {-2} \right),3-1} \right) = \left( {3,2} \right)$$

Nuestro vector \(\vec e\) acaba de ser escrito en base a nuestro sistema de referencia. Hay infinitos vectores en el plano con el mismo módulo, dirección y sentido, pero sólo uno que se apoya en el origen \(O\) de nuestro sistema de referencia. Al conjunto de todos los vectores con el mismo módulo, dirección y sentido se le llama vector libre.

Con las consideraciones anteriores la ecuación vectorial de la recta que pasa por el punto \(A\) con la dirección de un vector \(\vec e\), \(\overrightarrow {OX} = \overrightarrow {OA} \, + \lambda \vec e\,,\,\,\lambda \in\mathbb{R} \), adquiere todo su sentido.

Si la ecuación vectorial la expresamos en coordenadas tenemos:

$$\left( {x,y} \right) = \left( {a,b} \right) + \lambda \left( {{e_1},{e_2}} \right) \Rightarrow \left( {x,y} \right) = \left( {a,b} \right) + \left( {\lambda {e_1},\lambda {e_2}} \right) \Rightarrow \left( {x,y} \right) = \left( {a + \lambda {e_1},b + \lambda {e_2}} \right)$$

Igualando coordenadas:

$$\left\{ \begin{array}{l} x = a + \lambda {e_1}\\ y = b + \lambda {e_2} \end{array} \right.$$

Las ecuaciones anteriores reciben el nombre de ecuaciones paramétricas de la recta. De éstas, si despejamos el parámetro \(\lambda\) en ambas e igualamos, obtenemos la ecuación continua de la recta:

$$\begin{cases} \lambda = \dfrac{x-a}{e_1} \\[0.2cm] \lambda = \dfrac{y-b}{e_2} \end{cases} \Rightarrow \frac{x-a}{e_1} = \frac{y-b}{e_2}$$

Si ahora eliminamos denominadores y pasamos todo al primer miembro tenemos:

$${e_2}x-{e_2}a = {e_1}y-{e_1}b \Rightarrow {e_2}x-{e_1}y + {e_1}b-{e_2}a = 0$$

Si llamamos \(A = {e_2}\), \(B = -{e_1}\) y \(C = {e_1}b-{e_2}a\) tenemos la ecuación general o implícita de la recta:

$$Ax+By+C=0$$

Obsérvese que un vector director de la recta es \(\left( {{e_1},{e_2}} \right) = \left( {-B,A} \right)\) y que haciendo \(x=0\) se obtiene \(y=-\dfrac{C}{B}\) (conocida como ordenada en el origen), con lo que un punto de la recta (el que corta al eje \(Y\)) es \(\left( {0,-\dfrac{C}{B}} \right)\).

Volviendo a nuestro primer ejemplo, en el que considerábamos la recta \(2x-y+3=0\), tenemos que un vector director suyo es \(\left( {-B,A} \right) = \left( {1,2} \right)\) y que un punto suyo es \(\left( {0,-\dfrac{C}{B}} \right) = \left( {0,3} \right)\). Así obtenemos la ecuación vectorial \(\left( {x,y} \right) = \lambda \left( {1,2} \right) + \left( {0,3} \right)\), ecuación que ya habíamos deducido en su momento.

---

Puedes ver y descargar el artículo en formato pdf aquí.

La sabiduría viene de escuchar; de hablar, el arrepentimiento

Proverbio italiano

---

Cuando se estudian las matemáticas a un nivel básico en la secundaria, una de las cosas que primero se aprende a resolver es una ecuación de primer grado. A continuación, se puede introducir sin mucha dificultad el concepto de sistema lineal de dos ecuaciones con dos incógnitas. La forma, digamos reducida, de un sistema de este tipo es:

\[\begin{cases}a_1x+b_1y=c_1\\a_2x+b_2y=c_2\end{cases}\]

Los números reales \(a_1\), \(a_2\), \(b_1\), \(b_2\) reciben el nombre de coeficientes y los números \(c_1\) y \(c_2\) son los términos independientes del sistema (parecido a la nomenclatura estudiada en las expresiones algebraicas, monomios y polinomios). Las incógnitas o números reales de los cuales deseamos saber si satisfacen ambas ecuaciones, son \(x\) e \(y\).

Básicamente existen tres métodos para resolver este tipo de ecuaciones: sustitución, igualación y reducción.

El primero de ellos, el de sustitución, consiste en despejar una de las dos incógnitas de cualquiera de las dos ecuaciones y sustituirla en la otra.

Por ejemplo, dado el sistema

\[\begin{cases}2x+3y=4\\5x-2y=-9\end{cases}\]

despejamos la incógnita \(y\) de la primera ecuación, \(y=\dfrac{4-2x}{3}\), y la sustituimos en la segunda:

\[5x-2\frac{4-2x}{3}=-9\Rightarrow15x-2(4-2x)=-27\Rightarrow\]

\[\Rightarrow15x-8+4x=-27\Rightarrow19x=-19\Rightarrow x=-1\]

Sustituyendo el valor de \(x\) en la igualdad donde está la incógnita \(y\) despejada obtenemos:

\[y=\frac{4-2\cdot(-1)}{3}=\frac{4+2}{3}=\frac{6}{3}\Rightarrow y=2\]

Los sistemas lineales se caracterizan porque la representación gráfica de cada una de las dos ecuaciones es una recta. Si ambas se cortan, el punto de corte es la solución del sistema. En el caso del ejemplo anterior la representación gráfica queda reflejada en la figura siguiente.

En un sistema de ecuaciones no lineal con dos incógnitas, al menos una de las dos ecuaciones no es lineal, es decir, su representación gráfica no es una recta. Este tipo de sistemas se suelen resolver por el método de sustitución, método cuyo uso se ha visto en el ejemplo anterior para un sistema lineal. Veamos ahora un ejemplo de resolución de un sistema de ecuaciones no lineal.

Consideremos el sistema dado en la imagen que encabeza este artículo:

\[\begin{cases}x^2-2y^2=1\\xy=6\end{cases}\]

Despejando \(y\) de la segunda ecuación tenemos \(y=\dfrac{6}{x}\). Y sustituyendo este valor en la primera ecuación:

\[x^2-2\left(\frac{6}{x}\right)^2=1\Rightarrow x^2-\frac{72}{x^2}=1\]

Esta última es una ecuación racional, ya que la incógnita aparece en un denominador. Multiplicando ahora todos los términos por \(x^2\) llegamos a una ecuación bicuadrada:

\[x^4-72=x^2\Rightarrow x^4-x^2-72=0\]

Hagamos el cambio de variable \(x^2=z\) para obtener una ecuación de segundo grado:

\[z^2-z-72=0\Rightarrow z=\frac{1\pm\sqrt{(-1)^2-4\cdot1\cdot(-72)}}{2\cdot1}=\frac{1\pm\sqrt{1+288}}{2}=\]

\[=\frac{1\pm\sqrt{289}}{2}=\frac{1\pm17}{2}=\begin{cases}z_1=9\\z_2=-8\end{cases}\]

Deshaciendo ahora el cambio \(x^2=z\) obtenemos las soluciones de para la incógnita \(x\). Así, si \(z=9\), entonces tenemos dos soluciones para \(x\): \(x_1=3\) y \(x_2=-3\). Si \(z=-8\), la ecuación \(x^2=-8\) no proporciona soluciones reales para \(x\). Cada una de las dos soluciones anteriores para \(x\), \(x_1=3\) y \(x_2=-3\), proporcionan sendas soluciones para \(y\) sustituyendo en la fórmula donde habíamos despejado la incógnita \(y\) al comienzo de este método de sustitución, \(y=\dfrac{6}{x}\). Es decir si \(x_1=3\), entonces \(y_1=2\). Y si \(x_2=-3\), entonces \(y_2=-3\).

Resumiendo, y escribiendo las soluciones en forma de pares ordenados, el sistema no lineal tiene dos soluciones:

\[(3,\ 2)\quad\text{;}\quad(-3,\ -2)\]

Estos dos puntos del plano son los puntos donde se cortan las curvas \(x^2-2y^2=1\), \(xy=6\).

En esta página puedes encontrar una relación de ejercicios de sistemas no lineales, entre otras relaciones de ejercicios de matemáticas. Contiene las soluciones finales de cada uno de ellos. Además, también hay algunos problemas cuya solución se obtiene en muchos casos planteando un sistema de ecuaciones no lineal con dos incógnitas.

El genio se descubre en la fortuna adversa; en la prosperidad se oculta

Homero

---

En Matemáticas I (1º de Bachillerato) se trabaja mucho la demostración de identidades trigonométricas, la simplificación de expresiones en las que aparecen razones trigonométricas, la resolución de ecuaciones trigonométricas y de sistemas de ecuaciones trigonométricas. Veamos unos ejemplos.

Identidades trigonométricas

Para demostrar identidades trigonométricas, una técnica es comenzar por el lado de la igualdad que aparentemente sea más «largo» o «complicado» y, a través de sucesivos pasos usando las fórmulas trigonométricas que se saben (se pueden llevar al examen), intentar llegar a la otra parte de la igualdad. Veamos un par de ejemplos.

Demostrar las siguientes identidades trigonométricas:

a) $\displaystyle\frac{\cos x+\text{sen}\,x}{\cos x-\text{sen}\,x}-\frac{\cos x-\text{sen}\,x}{\cos x+\text{sen}\,x}=2\text{tg}\,x$

Solución

$\displaystyle\frac{\cos x+\text{sen}\,x}{\cos x-\text{sen}\,x}-\frac{\cos x-\text{sen}\,x}{\cos x+\text{sen}\,x}=$

$=\displaystyle\frac{\left( \cos x+\text{sen}\,x \right)\left( \cos x+\text{sen}\,x \right)}{\left( \cos x-\text{sen}\,x \right)\left( \cos x+\text{sen}\,x \right)}-\frac{\left( \cos x-\text{sen}\,x \right)\left( \cos x-\text{sen}\,x \right)}{\left( \cos x-\text{sen}\,x \right)\left( \cos x+\text{sen}\,x \right)}=$

$=\displaystyle\frac{{{\cos }^{2}}x+2\cos x\,\text{sen}\,x+\text{se}{{\text{n}}^{2}}x}{\left( \cos x-\text{sen}\,x \right)\left( \cos x+\text{sen}\,x \right)}-\frac{{{\cos }^{2}}x-2\cos x\,\text{sen}\,x+\text{se}{{\text{n}}^{2}}x}{\left( \cos x-\text{sen}\,x \right)\left( \cos x+\text{sen}\,x \right)}=$

$=\displaystyle\frac{2\cos x\,\text{sen}\,x+2\cos x\,\text{sen}\,x}{\left( \cos x-\text{sen}\,x \right)\left( \cos x+\text{sen}\,x \right)}=\frac{\text{sen}\,2x+\text{sen}\,2x}{{{\cos }^{2}}x-\text{se}{{\text{n}}^{2}}x}=\frac{2\,\text{sen}\,2x}{\cos 2x}=2\,\text{tg}\,2x$

---

b) $\displaystyle\frac{\text{tg}\,x}{\cos^2x}=\frac{1+\text{tg}^2x}{\text{cotg}^2x}$

Solución

$\displaystyle\frac{1+\text{t}{{\text{g}}^{2}}x}{\text{cotg}\,x}=\frac{1+\displaystyle\frac{\text{se}{{\text{n}}^{2}}\,x}{{{\cos }^{2}}x}}{\displaystyle\frac{\cos x}{\text{sen}\,x}}=\frac{\displaystyle\frac{{{\cos }^{2}}x+\text{se}{{\text{n}}^{2}}\,x}{{{\cos }^{2}}x}}{\displaystyle\frac{\cos x}{\text{sen}\,x}}=\frac{\displaystyle\frac{1}{{{\cos }^{2}}x}}{\displaystyle\frac{\cos x}{\text{sen}\,x}}=$

$=\displaystyle\frac{\text{sen}\,x}{\cos x\cdot {{\cos }^{2}}x}=\frac{\text{sen}\,x}{\cos x}\cdot \frac{1}{\cos {{x}^{2}}}=\frac{\text{tg}\,x}{{{\cos }^{2}}x}$

---

Expresiones trigonométricas

Simplificar las siguientes expresiones trigonométricas:

a) $\displaystyle\frac{\text{sen}\,\alpha+\text{cotg}\,\alpha}{\text{tg}\,\alpha+\text{cosec}\,\alpha}$

Solución

$\displaystyle\frac{\text{sen}\,\alpha +\text{cotg}\,\alpha }{\text{tg}\,\alpha +\text{cosec}\,\alpha }=\frac{\text{sen}\,\alpha +\displaystyle\frac{\cos \alpha }{\text{sen}\,\alpha }}{\displaystyle\frac{\text{sen}\,\alpha }{\cos \alpha }+\frac{1}{\text{sen}\,\alpha }}=\frac{\displaystyle\frac{\text{se}{{\text{n}}^{2}}\,\alpha +\cos \alpha }{\text{sen}\,\alpha }}{\displaystyle\frac{\text{se}{{\text{n}}^{2}}\,\alpha +\cos \alpha }{\cos \alpha \,\text{sen}\,\alpha }}=$

$=\displaystyle\frac{\left( \text{se}{{\text{n}}^{2}}\,\alpha +\cos \alpha \right)\cos \alpha \,\text{sen}\,\alpha }{\left( \text{se}{{\text{n}}^{2}}\,\alpha +\cos \alpha \right)\,\text{sen}\,\alpha }=\cos \alpha$

---

b) $\displaystyle2\text{tg}\,\alpha\cdot\cos^2\frac{\alpha}{2}-\text{sen}\,\alpha$

Solución

$\displaystyle2\,\text{tg}\,\alpha \cdot {{\cos }^{2}}\frac{\alpha }{2}-\text{sen}\,\alpha =2\frac{\text{sen}\,\alpha }{\cos \alpha }\cdot \frac{1+\cos \alpha }{2}-\text{sen}\,\alpha =\frac{\text{sen}\,\alpha \left( 1+\cos \alpha \right)}{\cos \alpha }-\text{sen}\,\alpha =$

$=\displaystyle\frac{\text{sen}\,\alpha +\text{sen}\,\alpha \cos \alpha }{\cos \alpha }-\frac{\text{sen}\,\alpha \cos \alpha }{\cos \alpha }=\frac{\text{sen}\,\alpha }{\cos \alpha }=\text{tg}\,\alpha$

---

Ecuaciones trigonométricas

Resolver las siguientes ecuaciones trigonométricas y dar las soluciones dentro del intervalo \(\left[ 0{}^\text{o}\,,\,360{}^\text{o} \right)\) (primera vuelta):

a) $\displaystyle\text{tg}\,x+2\text{sen}\,x=0$

Solución

$\displaystyle\text{tg}\,x+2\text{sen}\,x=0\Rightarrow \frac{\text{sen}\,x}{\cos x}+2\text{sen}\,x=0\Rightarrow \text{sen}\,x+2\text{sen}\,x\cos x=0\Rightarrow$

$\displaystyle\Rightarrow \text{sen}\,x\left( 1+2\cos x \right)=0\Rightarrow \begin{cases} \text{sen}\,x=0\Rightarrow x=0{}^\text{o}\,\,;\,\,x=180{}^\text{o}\\ \cos x=-\frac{1}{2}\Rightarrow x=120{}^\text{o}\,\,;\,\,x=240{}^\text{o} \end{cases}$

---

b) $\displaystyle\text{sen}\,x\cdot\text{tg}\,x=\frac{\sqrt{3}}{2}$

Solución

$\displaystyle\text{sen }x\cdot \text{tg}\,x=\frac{\sqrt{3}}{6}\Rightarrow \text{sen}\,x\cdot \frac{\text{sen}\,x}{\cos x}=\frac{\sqrt{3}}{6}\Rightarrow$

$\displaystyle \Rightarrow 6\,\text{se}{{\text{n}}^{2}}\,x=\sqrt{3}\cos x\Rightarrow 6\left( 1-{{\cos }^{2}}x \right)=\sqrt{3}\cos x\Rightarrow$

$\displaystyle\Rightarrow 6-6{{\cos }^{2}}x=\sqrt{3}\cos x\Rightarrow 6{{\cos }^{2}}x+\sqrt{3}\cos x-6=0$

El discriminante de la ecuación anterior es $\displaystyle\Delta=\sqrt{3}^2-4\cdot6\cdot(-6)=3+144=147$, y $\sqrt{147}=\sqrt{7^2\cdot3}=7\sqrt{3}$. Por tanto:

$\displaystyle\cos x=\dfrac{-\sqrt{3}\pm7\sqrt{3}}{2\cdot6}=\dfrac{-\sqrt{3}(-1\pm7)}{12}=\begin{cases}\frac{6\sqrt{3}}{12}=\frac{\sqrt{3}}{2}\\ \frac{-8\sqrt{3}}{12}=\frac{-2\sqrt{3}}{3}\end{cases}$

Si $\cos x=\dfrac{\sqrt{3}}{2}$, entonces $x=30{}^\text{o}\,\,;\,\,x=330{}^\text{o}$.

Si $\cos x=\dfrac{-2\sqrt{3}}{3}$, entonces no existe solución para $x$ pues $\dfrac{-2\sqrt{3}}{3}\cong -1,15$, y el coseno no puede ser un número menor que $-1$.

---

Sistema de ecuaciones trigonométricas

Resuelve el siguiente sistema de ecuaciones trigonométricas, dando las soluciones en el primer cuadrante.

$\displaystyle\begin{cases}\text{sen}\,x\cdot\text{sen}\,y=\displaystyle\frac{\sqrt{2}}{4}\\ \displaystyle\cos x\cdot\text{sen}\,y=\frac{\sqrt{6}}{4}\end{cases}$

Solución

Dividiendo ambas ecuaciones tenemos:

$\displaystyle\frac{\text{sen}\,x}{\cos x}=\frac{\displaystyle\frac{\sqrt{2}}{4}}{\displaystyle\frac{\sqrt{6}}{4}}\Rightarrow \text{tg}\,x=\frac{4\sqrt{2}}{4\sqrt{6}}\Rightarrow \text{tg}\,x=\sqrt{\frac{2}{6}}\Rightarrow$

$\displaystyle\Rightarrow \text{tg}\,x=\sqrt{\frac{1}{3}}\Rightarrow \text{tg}\,x=\frac{\sqrt{3}}{3}\Rightarrow x=30{}^\text{o}$

Sustituyendo en la primera ecuación:

$\displaystyle\text{sen}\,30{}^\text{o}\cdot \text{sen}\,y=\frac{\sqrt{2}}{4}\Rightarrow \frac{1}{2}\text{sen}\,y=\frac{\sqrt{2}}{4}\Rightarrow \text{sen}\,y=\frac{2\sqrt{2}}{4}\Rightarrow \text{sen}\,y=\frac{\sqrt{2}}{2}\Rightarrow y=45{}^\text{o}$

---

Nada está perdido si se tiene por fin el valor de proclamar que todo esta perdido y que hay que empezar de nuevo

Julio Cortázar

---

Cuando se comienza a trabajar la trigonometría, la medida de los ángulos que se utiliza es el grado sexagesimal. Esta medida proviene de la antigua Babilonia. Los babilonios supusieron, en un principio, que el año tenía 360 días y tomaron como medida angular «el recorrido diario del sol alrededor de la Tierra». Esta forma de medir ha perdurado hasta nuestros días y su influencia se ha dejado notar, también, en la medición del tiempo.

Un grado sexagesimal es, por tanto, cada una de las 360 partes iguales en las que se divide una circunferencia. Cada grado se divide en 60 minutos, y cada minuto en 60 segundos.

Otra medida de los ángulos es el radián.

Definición

Si se toma cualquier circunferencia de radio \(r=\overline{OA}\) y se lleva esta longitud \(r\) sobre un arco de la circunferencia, es decir, \(r=\overline{OA}=\text{longitud}\,AB\), el ángulo central \(\alpha\) determinado por el arco y sus radios mide un radián: \(1\,\text{rad}\).

Relación entre grados sexagesimales y radianes

Para calcular a cuántos radianes equivale un ángulo completo de \(360^{\text{o}}\), basta con aplicar una sencilla relación de proporcionalidad directa. Dibujamos una circunferencia de radio \(r\) . Si a un arco de longitud \(r\) le corresponde un radián, a un arco de longitud la longitud de la circunferencia, \(2\pi r\) , le corresponderán \(x\) radianes. Es decir:

\[\frac{r}{2\pi r}=\frac{1}{x}\Rightarrow x=\frac{2\pi r}{r}=2\pi\]

Esto quiere decir que a un ángulo completo de \(360^{\text{o}}\) le corresponden \(2\pi\) radianes, o lo que es lo mismo, a un ángulo de \(180^{\text{o}}\) le corresponden \(\pi\) radianes. De este modo, para convertir un ángulo dado en grados, \(\alpha^{\text{o}}\), en radianes, \(\alpha\,\text{rad}\), o viceversa, basta con utilizar la siguiente proporción:

\[\frac{\alpha^{\text{o}}}{\alpha\,\text{rad}}=\frac{180^{\text{o}}}{\pi}\]

Veamos como ejemplo a cuantos grados sexagesimales equivale un radián:

\[\frac{\alpha^{\text{o}}}{1\,\text{rad}}=\frac{180^{\text{o}}}{\pi}\Rightarrow \alpha=\frac{1\cdot180}{\pi}\cong57,296^{\text{o}}\]

O sea, un radián es igual, aproximadamente, a \(57,296^{\text{o}}\).

Uso de la calculadora

Para hallar las razones trigonométricas de un ángulo dado en radianes hay que empezar poniendo la calculadora en el modo radianes: MODE RAD. Cada calculadora tiene una combinación de teclas propia para pasar al modo radianes. Normalmente una calculadora viene en modo grados sexagesimales: MODE DEG, que suele venir indicado con una D, o la abreviatura DEG en la parte superior. Cuando pasamos al modo radianes con la combinación de teclas adecuada, en la parte superior aparecerá una R o la abreviatura RAD. En estos momentos ya está lista la calculadora para hacer cálculos en radianes. Veamos un ejemplo.

Con la calculadora en el modo grados sexagesimales es muy fácil obtener que \(\text{sen}\,72^{\text{o}}\cong0,951\). Para ver que obtenemos el mismo valor en radianes, pasaremos \(72^{\text{o}}\) a radianes, y luego calcularemos el seno del valor obtenido, ya con la calculadora en el modo radianes.

\[\frac{72^{\text{o}}}{x\,\text{rad}}=\frac{180^{\text{o}}}{\pi}\Rightarrow x=\frac{72\cdot\pi}{180}=\frac{2\pi}{5}\text{rad}\]

Ahora, con la calculadora en modo radianes, podemos comprobar también que \(\text{sen}\dfrac{2\pi}{5}\cong0,951\).

La imaginación es la voz del atrevimiento

Henry Miller

---

El determinante de una matriz cuadrada $A$ es un número real asociado a dicha matriz, al que denotaremos del siguiente modo: $|A|$.

Sea $A$ una matriz cuadrada de orden dos. Su determinante es muy fácil de calcular:

\[|A|=\begin{vmatrix}
a_{11} &a_{12} \\
a_{21} &a_{22}
\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}\]

Si $A$ es una matriz cuadrada de orden tres, su determinante se calcula del siguiente modo:

\[|A|=\begin{vmatrix}
a_{11} & a_{12} & a_{13}\\
a_{21} & a_{22} & a_{23}\\
a_{31} & a_{32} & a_{33}
\end{vmatrix}=\]

\[=(a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}) -(a_{13}a_{22}a_{31}+a_{12}a_{21}a_{33}+a_{11}a_{23}a_{32})\]

Hay una regla para recordar fácilmente la fórmula anterior, denomimada regla de Sarrus.

Cuando el determinante es de orden mayor que tres no queda más remedio que desarrollar por una fila o por una columna:

Si los elementos de una fila o de una columna de una matriz cuadrada se multiplican por sus respectivos adjuntos y se suman los resultados, se obtiene el determinante de la matriz inicial. Se dice entonces que el determinante está desarrollado por los elementos de esa fila o de esa columna.

Más concretamente, si $A=(a_{ij})$ es una matriz cuadrada de orden $n$, el determinante de $A$ se puede obtener del siguiente modo:

$$\left| A \right| = {a_{i1}}{A_{i1}} + {a_{i2}}{A_{i2}} + \ldots + {a_{in}}{A_{in}}$$

si se desarrolla por la fila i-ésima, o bien:

$$\left| A \right| = {a_{1j}}{A_{1j}} + {a_{2j}}{A_{2j}} + \ldots + {a_{nj}}{A_{nj}}$$

si se desarrolla por la columna j-ésima.

En los desarrollos anteriores $A_{ij}$ es el adjunto del elemento $a_{ij}$. Y, si llamamos $\Delta_{ij}$ al menor complementario del elemento $a_{ij}$ (es decir, al determinante que resulta de eliminar la fila $i$ y la columna $j$), recodemos que el adjunto coincide con el menor complementario si $i+j$ es par, y con el opuesto del menor complementario si $i+j$ es impar. Hay una fórmula para describir todo esto:

$$A_{ij}=(-1)^{i+j}\Delta_{ij}$$

Para más información sobre el menor complementario y el adjunto de un elemento de una matriz se puede consultar este artículo dedicado al cálculo de matrices inversas.

Naturalemente, el desarrollo anterior es independiente de la fila o de la columna elegidas.

Por ejemplo, calculemos el determinante de la matriz $A=\begin{pmatrix}1&2&0&-3\\4&-1&1&-2\\0&3&2&-1\\ -2&1&3&2 \end{pmatrix}$.

No importa la fila o la columna que elijamos, pero al hacer el desarrollo por la elegida, cada uno de sus elementos se multiplica por su adjunto y luego se suma todo. Por tanto, siempre será mejor si elegimos una fila o una columna con el mayor número de ceros posible.

Desarrollando por la primera fila se tiene:

$$|A|=1\cdot A_{11}+2\cdot A_{12}+0\cdot A_{13}+(-3)\cdot A_{14}=\Delta_{11}-2\cdot \Delta_{12}+3\cdot\Delta_{14}=$$

$$=\begin{vmatrix}-1&1&-2\\3&2&-1\\1&3&2\end{vmatrix}-2\cdot\begin{vmatrix}4&1&-2\\0&2&-1\\-2&3&2\end{vmatrix}+3\cdot\begin{vmatrix}4&-1&1\\0&3&2\\-2&1&3 \end{vmatrix}=$$

$$=-28-2\cdot22+3\cdot38=-28-44+114=42$$

Puedes desarrollar por cualquier otra fila o columna. Se llega al mismo resultado.

Propiedades de los determinantes

1. El determinante de una matriz triangular es el producto de sus elementos diagonales. En particular, $|I|=1$, donde $I$ es la matriz identidad.
2. El determinande de una matriz cuadrada es igual que el de su traspuesta: $|A|=|A^t|$.
3. Si en una matriz cuadrada todos los elementos de una fila o de una columna son ceros, su determinante es cero.
4. Si se permutan o se intercambian entre si dos filas o dos columnas de una matriz cuadrada, su determinante cambia de signo.
5. Si una matriz cuadrada tienen dos filas o dos columnas proporcionales, su determinante es cero. En particular, si una matriz cuadrada tiene dos filas o dos columnas iguales, su determinante es cero.
6. Si multiplicamos por el mismo número todos los elementos de una fila o de una columna de una matriz cuadrada, su determinante queda multiplicado por ese número. Consecuentemente, el determinante de una matriz cuadrada $A$ de orden $n$ multiplicada por un escalar $\lambda$, es igual a $\lambda^n$ veces el determinante de $A$. Es decir: $|\lambda A|=\lambda^n|A|$.
7. Si denotamos por $c_1,\ldots,c_i,\ldots,c_n$ a las $n$ columnas de una matriz cuadrada de orden $n$, se tiene que $|c_1,\ldots,c_i+c_i’,\ldots,c_n|=|c_1,\ldots,c_i,\ldots,c_n|+|c_1,\ldots,c_i’,\ldots,c_n|$, siendo esta descomposición válida cualesquiera sean la fila o la columna en la que se encuentre los sumandos.
8. Si una matriz tiene una fila o una columna que es combinación lineal de las demás filas o columnas, entonces su determinante es cero. Y, recíprocamente, si un determinate es cero, entonces tiene una fila (y una columna) que es combinación lineal de las demás.
9. El determinante no varía si a una fila o a una columna se le suma una combinación lineal de las demás. En particular, si a una fila o a una columna se le suma o se le resta otra previamente multiplicada por un número, el determinante no varía.
10. El determinante del producto de dos matrices cuadradas es igual al producto de sus determinantes: $|A\cdot B|=|B\cdot A|=|A|\cdot|B|$.

Se dice que una matriz cuadrada $A$ es regular o invertible si tiene inversa o, equivalentemente, si $|A|\neq0$. En tal caso, se tiene que $\left|A\right|^{-1}=\dfrac{1}{|A|}$. La demostración es muy sencilla. Como $AA^{-1}=I$, tenemos:

$$\left|AA^{-1}\right|=|I|\Rightarrow|A|\left|A^{-1}\right|=1\Rightarrow\left|A\right|^{-1}=\dfrac{1}{|A|}$$

Para calcular un determinante usando el desarrollo por una fila o columna, a veces es conveniente, y de manera previa, «hacer ceros» en casi todos los términos de la fila o de la columna por la que vayamos a desarrollar. En estos casos hay que utilizar con cierto ingenio algunas de las propiedades de los determinantes, anteriormente enumeradas. Veámoslo volviendo a calcular el determinante del ejemplo anterior.

En el ejemplo realizado anteriormente, hemos desarrollado por la primera fila y hemos obtenido que $|A|=42$. Pero antes de hacer el desarrollo podemos hacer algunos cambios y todo será más fácil.

Recordemos que teníamos que calcular el siguiente determinante:

$$\begin{vmatrix}1&2&0&-3\\4&-1&1&-2\\0&3&2&-1\\ -2&1&3&2 \end{vmatrix}$$

Si a la segunda fila le restamos la primera multiplicada por $4$, y a la cuarta fila le sumamos la primera multiplicada por $2$, en virtud de la propiedad 9, tenemos:

$$\begin{vmatrix}1&2&0&-3\\4&-1&1&-2\\0&3&2&-1\\ -2&1&3&2 \end{vmatrix} =\begin{vmatrix}1&2&0&-3\\0&-9&1&10\\0&3&2&-1\\ 0&5&3&-4 \end{vmatrix}=1\cdot A_{11}=\Delta_{11}=\begin{vmatrix} -9&1&10\\ 3&2&-1\\ 5&3&-4 \end{vmatrix}=$$

$$=(72-5+90)-(100-12+27)=157-115=42$$

Ejercicios resueltos

1. Obtener el valor de los siguientes determinantes usando, previamente, las propiedades de estos. Posteriormente puedes desarrollar por los elementos de una fila o de una columna.

a) $\begin{vmatrix} 1 & 1 & 1 & 1 & 1\\ 1 & 3 & 3 & 3 & 3\\ 1 & 3 & 5 & 5 & 5\\ 1 & 3 & 5 & 7 & 7\\ 1 & 3 & 5 & 7 & 9\\ \end{vmatrix}$

Solución

Restando a la quinta fila la cuarta, a la cuarta la tercera, a la tercera la segunda y a la segunda la primera, resulta ser el determinande de una matriz triangular, cuyo valor es el producto de los elementos de la diagonal principal (basta desarrollar por los elementos de la primera columna):

$\begin{vmatrix} 1 & 1 & 1 & 1 & 1\\ 1 & 3 & 3 & 3 & 3\\ 1 & 3 & 5 & 5 & 5\\ 1 & 3 & 5 & 7 & 7\\ 1 & 3 & 5 & 7 & 9 \end{vmatrix}=\begin{vmatrix} 1 & 1 & 1 & 1 & 1\\ 0 & 2 & 2 & 2 & 2\\ 0 & 0 & 2 & 2 & 2\\ 0 & 0 & 0 & 2 & 2\\ 0 & 0 & 0 & 0 & 2 \end{vmatrix}=1\cdot2\cdot2\cdot2\cdot2=16$.

---

b) $\begin{vmatrix} 1+x & 1 & 1 & 1\\ 1 & 1-x & 1 & 1\\ 1 & 1 & 1+y & 1\\ 1 & 1 & 1 & 1-y\\ \end{vmatrix}$

Solución

Restando a cada fila la siguiente y sacando factor común $x$ de la primera fila e $y$ de la tercera, se tiene:

$\begin{vmatrix} 1+x & 1 & 1 & 1\\ 1 & 1-x & 1 & 1\\ 1 & 1 & 1+y & 1\\ 1 & 1 & 1 & 1-y\end{vmatrix}=\begin{vmatrix} x & x & 0 & 0\\ 0 & -x & -y & 0\\ 0 & 0 & y & y\\ 1 & 1 & 1 & 1-y\end{vmatrix}=x\cdot y\cdot\begin{vmatrix} 1 & 1 & 0 & 0\\ 0 & -x & -y & 0\\ 0 & 0 & 1 & 1\\ 1 & 1 & 1 & 1-y\end{vmatrix}$

Ahora, en el último determinante, restando a la cuarta fila la primera y desarrollando por la primera columna:

$=x\cdot y\cdot\begin{vmatrix} 1 & 1 & 0 & 0\\ 0 & -x & -y & 0\\ 0 & 0 & 1 & 1\\ 0 & 0 & 1 & 1-y\end{vmatrix}=x\cdot y\cdot\begin{vmatrix} -x & -y & 0\\ 0 & 1 &1\\ 0 & 1 & 1-y\end{vmatrix}=x\cdot y\cdot(-x)\cdot\begin{vmatrix}1 & 1\\1 & 1-y\end{vmatrix}=$

$=x\cdot y\cdot(-x)\cdot(1-y-1)=x\cdot y\cdot(-x)\cdot(-y)=x^2\cdot y^2$.

---

c) $\begin{vmatrix} x^2+1 & xy & xz\\ xy & y^2+1 & yz\\ xz & yz & z^2+1\\ \end{vmatrix}$

Solución

Multiplicando la segunda y tercera filas por \(x\):

$\begin{vmatrix} x^2+1 & xy & xz\\ xy & y^2+1 & yz\\ xz & yz & z^2+1\end{vmatrix}=\dfrac{1}{x^2}\begin{vmatrix} x^2+1 & xy & xz\\ x^2y & xy^2+x & xyz\\ x^2z & xyz & xz^2+x\end{vmatrix}=$

Restando a la segunda fila la primera multiplicada por \(y\), y restando a la tercera fila la primera multiplicada por \(x\):

$=\dfrac{1}{x^2}\begin{vmatrix} x^2+1 & xy & xz\\ -y & x & 0\\ -z & 0 & x\end{vmatrix}=$

Sacando factor común \(x\) en la segunda y tercera columna y desarrollando por la regla de Sarrus:

$=\dfrac{1}{x^2}\cdot x^2\cdot \begin{vmatrix} x^2+1 & y & z\\ -y & 1 & 0\\ -z & 0 & 1\end{vmatrix}=(x^2+1)-(-z^2-y^2)=x^2+y^2+z^2+1$.

---

d) $\begin{vmatrix} x & y & x+y\\ y & x+y & x\\ x+y & x & y\\ \end{vmatrix}$

Solución

Sumando las filas segunda y tercera a la primera:

$\begin{vmatrix} x & y & x+y\\ y & x+y & x\\ x+y & x & y\end{vmatrix}=\begin{vmatrix} 2x+2y & 2x+2y & 2x+2y\\ y & x+y & x\\ x+y & x & y\end{vmatrix}=2(x+y)\begin{vmatrix} 1 & 1 & 1\\ y & x+y & x\\ x+y & x & y\end{vmatrix}$

Restando a la segunda columna la primera y a la tercera columna la primera

$=2(x+y)\begin{vmatrix} 1 & 0 & 0\\ y & x & x-y\\ x+y & -y & -x\end{vmatrix}=2(x+y)\begin{vmatrix}x&x-y\\-y&-x\end{vmatrix}=$

$=2(x+y)\left(-x^2-(-y(x-y)\right)=2(x+y)(-x^2+xy-y^2)=$

$=2(-x^3+x^2y-xy^2-x^2y+xy^2-y^3)=-2(x^3+y^3)$.

---

2. Sabiendo que $\begin{vmatrix} a & b & c\\ p & q & r\\ x & y & z\\ \end{vmatrix}=7$, usa las propiedades de los determinantes para calcular el valor de los dos siguientes:

$$\begin{vmatrix} a+2x & b+2y & c+2z\\ p & q & r\\ 2x+p & 2y+q & 2z+r\\ \end{vmatrix}\quad;\quad \begin{vmatrix} -b & c+b & 5a\\ -q & r+q & 5p\\ -y & z+y & 5x\\ \end{vmatrix}$$

Solución

Primer determinante.

$\begin{vmatrix} a+2x & b+2y & c+2z\\ p & q & r\\ 2x+p & 2y+q & 2z+r\\ \end{vmatrix}\overset{\underset{\mathrm{\textbf{(1)}}}{}}{=}\begin{vmatrix} a & b & c\\ p & q & r\\ 2x+p & 2y+q & 2z+r\\ \end{vmatrix}+\begin{vmatrix} 2x & 2y & 2z\\ p & q & r\\ 2x+p & 2y+q & 2z+r\\ \end{vmatrix}\overset{\underset{\mathrm{\textbf{(2)}}}{}}{=}$

$\overset{\underset{\mathrm{\textbf{(2)}}}{}}{=}\begin{vmatrix} a & b & c\\ p & q & r\\ 2x & 2y & 2z\\ \end{vmatrix}+\begin{vmatrix} a & b & c\\ p & q & r\\ p & q & r\\ \end{vmatrix}+\begin{vmatrix} 2x & 2y & 2z \\ p & q & r\\ p & q & r \end{vmatrix}+\begin{vmatrix} 2x & 2y & 2z\\ p & q & r\\ p & q & r \end{vmatrix}\overset{\underset{\mathrm{\textbf{(3)}}}{}}{=}$

$\overset{\underset{\mathrm{\textbf{(3)}}}{}}{=}2\cdot\begin{vmatrix} a & b & c\\ p & q & r\\ x & y & 2\ \end{vmatrix}+0+0+0=2\cdot7=14$

En los pasos $\textbf{(1)}$ y $\textbf{(2)}$ se ha utilizado la propiedad 7.

En el paso $\textbf{(3)}$ se ha utilizado la propiedad 6 (sacando factor el $2$ del primer determinante porque es común en la tercera fila) y la propiedad 5 (los tres últimos determinantes son cero porque tienen dos filas iguales).

Segundo determinante.

$\begin{vmatrix} -b & c+b & 5a\\ -q & r+q & 5p\\ -y & z+y & 5x \end{vmatrix}\overset{\underset{\mathrm{\textbf{(1)}}}{}}{=}\begin{vmatrix} -b & c & 5a\\ -q & r & 5p\\ -y & z & 5x \end{vmatrix}+\begin{vmatrix} -b & b & 5a\\ -q & q & 5p\\ -y & y & 5x \end{vmatrix}\overset{\underset{\mathrm{\textbf{(2)}}}{}}{=}(-1)\cdot5\cdot\begin{vmatrix} b & c & a\\ q & r & p\\ y & z & x \end{vmatrix}+0\overset{\underset{\mathrm{\textbf{(3)}}}{}}{=}$

$\overset{\underset{\mathrm{\textbf{(3)}}}{}}{=}-5\cdot\begin{vmatrix} a & b & c\\ p & q & r\\ x & y & z \end{vmatrix}=-5\cdot7=-35$

En el paso $\textbf{(1)}$ se ha utilizado la propiedad 7.

En el paso $\textbf{(2)}$ se ha utilizado la propiedad 6 (sacando factor el $-1$ y el $5$ determinante porque son comunes en la primera y tercera columnas, respectivamente), y la propiedad 5 (el segundo determinante es cero porque la primera y segunda columnas son proporcionales.

En el paso $\textbf{(3)}$ se ha utilizado la propiedad 4 dos veces: se ha intercambiado la primera columna con la tercera, y luego la segunda columna con la tercera. Como hay dos intercambios, hay dos cambios de signo, con lo que el signo del determinante permanece.

---

En la vida hay algo peor que el fracaso: el no haber intentado nada

Franklin Delano Roosevelt

---

Por definición, el rango de una matriz es igual al número de filas linealmente independientes. Como en estos apuntes no vamos a hablar de independencia lineal, vamos a usar los determinantes para calcular el rango de una matriz. Antes, es necesario que hagamos algunas definiciones.

Submatrices y menores

Supongamos que $A$ es una matriz de orden $m\times n$, es decir, con $m$ filas y $n$ columnas: $A\in\mathfrak{M}_{m\times n}$.

• Se llama submatriz de $A$ a cualquier matriz que se obtenga a partir de $A$ suprimiendo filas y columnas.
• Si una submatriz de $A$ es cuadrada de orden $k$, a su determinante se le denomina menor de orden $k$ de $A$.
• Al menor formado por las $k$ primeras filas y las $k$ primeras columnas de $A$ se le llama menor principal de orden $k$ y lo denotaremos por $\delta_k$. Nótese que, si $m=n$, es decir, si $A$ es cuadrada de orden $n$, entonces $\delta_n=|A|$.

Por ejemplo, dada la matriz $A=\begin{pmatrix}
2&1&-3&4\\
0&4&-4&5
\end{pmatrix}$, el menor principal de orden $2$ es $\delta_2=\begin{vmatrix}
2&1\\
0&4
\end{vmatrix}=8-0=8$.

Rango de una matriz

Sea $A\in\mathfrak{M}_{m\times n}$. El rango de la matriz $A$ es el mayor orden de los menores no nulos de $A$. Denotaremos por $r(A)$ al rango de la matriz $A$.

Propiedades del rango de una matriz

a) El rango de una matriz no varía si se intercambian entre sí dos filas o dos columnas.

b) Si una matriz $A$ tiene una fila o columna de ceros, el rango de  coincide con el rango de la matriz que se obtiene al suprimir esa fila o esa columna.

c) El rango de una matriz no cambia si se suprime una fila o una columna que sea combinación lineal de las restantes.

d) El rango de una matriz es igual al de su traspuesta: $r(A)=r\left(A^t\right)$.

e) Si $A$ es una matriz de orden $m\times n$, se tiene que $r(A)\leq\text{min}\{m\ ,n\}$. Es decir, el rango siempre es menor o a lo sumo igual que el número más pequeño de entre estos dos: número de filas y número de columnas. Así, por ejemplo, si una matriz es de orden $3\times 5$, su rango será a lo sumo $3$.

Merece la pena detenerse con un ejemplo, sobre todo para dejar constancia de la propiedad c) y explicar lo que significa que una fila sea combinación lineal de las restantes. Consideremos la siguiente matriz:

$$A=\begin{pmatrix}
3&1&-1&-2&1\\ 5&-3&5&0&9\\ 0&0&0&0&0 \\ 1&-2&3&1&4\\
\end{pmatrix}$$

Como $A$ tiene una fila de ceros (la tercera), según la propiedad b), el rango de la matriz anterior es igual al rango de esta otra, la cual se obtiene de la anterior suprimiendo la fila de ceros:

$$B=\begin{pmatrix}
3&1&-1&-2&1\\ 5&-3&5&0&9\\ 1&-2&3&1&4\\
\end{pmatrix}$$

Llamemos $f_1$, $f_2$ y $f_3$ a la fila 1, fila 2 y fila 3, respectivamente, de la matriz anterior. Entonces $2f_3+f_1=f_2$:

$$2\begin{pmatrix}1&-2&3&1&4\end{pmatrix}+\begin{pmatrix}3&1&-1&-2&1\end{pmatrix}=$$

$$=\begin{pmatrix}2&-4&6&2&8\end{pmatrix}+\begin{pmatrix}3&1&-1&-2&1\end{pmatrix}=\begin{pmatrix}5&-3&5&0&9\end{pmatrix}$$

Esto quiere decir que la fila 2 es combinación lineal (o simplemente combinación) de la fila 3 y la fila 1. Por tanto, según la propiedad c), podemos suprimir la fila 2 de la matriz anterior, con lo que su rango será igual al de esta otra:

$$C=\begin{pmatrix}
3&1&-1&-2&1\\ 1&-2&3&1&4\\
\end{pmatrix}$$

Según la propiedad e), como esta matriz es de orden $2\times5$, su rango será, a los sumo $2$: $r(A)\leq2$. De hecho, su rango es dos porque el menor principal de orden dos de esta matriz es distinto de cero: $\delta_1=\begin{vmatrix}
3&1\\ 1&-2 \end{vmatrix}=7\neq0$. Por tanto, finalmente tenemos que $r(A)=r(B)=r(C)=2$.

Ejemplos de distintos casos

Antes de ver un método general para hallar el rango de una matriz a partir de sus menores, veamos algunos ejemplos del cálculo del rango de una matriz según el orden de ésta:

Caso 1

$A$ es una matriz cuadrada de orden dos: $A=\begin{pmatrix}a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{pmatrix}$.

En este caso el único menor de orden dos es el menor principal, es decir, el determinante de la propia matriz $A$: $\delta_1=|A|$.

a) Si $\delta_1=|A|\neq0$, entonces $r(A)=2$. Por ejemplo, si $A=\begin{pmatrix}1&-2\\ 8&6\\ \end{pmatrix}$, entonces $r(A)=2$, ya que $|A|=10\neq0$.

b) Si $\delta_1=|A|=0$, el rango ya no puede ser igual a dos porque no habrá ningún menor de orden dos distinto de cero. Entonces, o bien $r(A)=1$, si hay algún término distinto de cero, $r(A)=0$, si todos los términos de la matriz son cero, es decir, si $A$ se trata de la matriz nula. Por ejemplo, si $A=\begin{pmatrix}2&-5\\ -4&10\\ \end{pmatrix}$, entonces $r(A)=1$, porque $|A|=0$, y hay términos distintos de cero en la matriz. Observa que el determinante será nulo cuando las dos filas sean proporcionales. En este caso la fila 2 es igual a la fila 1 multiplicada por $2$.

Caso 2

$A$ es una matriz de orden $2\times3$: $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ \end{pmatrix}$.

En este caso, la matriz $A$ tiene tres menores de orden dos:

$$\begin{vmatrix}a_{11}&a_{12}\\ a_{21}&a_{22}\\ \end{vmatrix}\quad ; \quad\begin{vmatrix}a_{11}&a_{13}\\ a_{21}&a_{23}\\ \end{vmatrix}\quad; \quad\begin{vmatrix}a_{12}&a_{13}\\ a_{22}&a_{23}\\ \end{vmatrix}$$

Si alguno de ellos es distinto de cero, $r(A)=2$. Si todos son cero, entonces el rango será uno (cuando algún término de la matriz sea distinto de cero) o será cero (cuando $A$ sea la matriz nula).

Por ejemplo, el rango de la matriz $A=\begin{pmatrix}-1&2&-5\\ 4&-8&6\\ \end{pmatrix}$ es dos porque contiene un menor de orden dos distinto de cero: $\begin{vmatrix}-1&-5\\ 4&6\\ \end{vmatrix}=-6+20=14\neq0$. Obsérvese que el menor principal es igual a cero: $\begin{vmatrix}-1&2\\ 4&-8\\ \end{vmatrix}=8-8=0$. Seguramente, sería con el primero que probaríamos. Pero, al ser cero, seguimos probando con el resto. En cuanto demos con uno que sea distinto de cero (como ocurre en este caso), el rango de la matriz ya es dos.

Caso 3

$A$ es una matriz de orden $3\times2$. Entonces, como su traspuesta es de orden $2\times3$, por la propiedad d), $r(A)=r\left(A^t\right)$, y se procede como en el caso anterior.

Caso 4

$A$ es una matriz de orden $2\times m$, con $m>3$ En este caso se procede como en el caso 2, lo que ocurre es que habrá más menores de orden dos.

Caso 5

$A$ es una matriz de orden $n\times2$, con $n>3$. En este caso se procede como en el caso 3.

Caso 6

$A$ es una matriz cuadrada de orden tres: $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{31}\\ \end{pmatrix}$.

En este caso el único menor de orden tres es el menor principal, es decir, el determinante de la propia matriz $A$: $\delta_1=|A|$.

a) Si $\delta_1=|A|\neq0$, entonces $r(A)=3$. Por ejemplo, si $A=\begin{pmatrix}1&2&-2\\ 0&-4&-1\\ -2&1&1\\ \end{pmatrix}$, entonces tenemos que $r(A)=3$, ya que

$$|A|=\begin{vmatrix}1&2&-2\\ 0&-4&-1\\ -2&1&1\\ \end{vmatrix}=(-4+4+0)-(-16+0-1)=0-(-17)=17\neq0$$

b) Si $\delta_1=|A|=0$, el rango ya no puede ser igual a tres porque no habrá ningún menor de orden tres distinto de cero. Entonces $r(A)\leq2$.

Por ejemplo, consideremos la matriz $A=\begin{pmatrix}1&3&-4\\ -1&-1&2\\ 0&2&-2\\ \end{pmatrix}$. Se tiene que $|A|=0$ (¡compruébalo!). De hecho, la tercera fila es la suma de las dos primeras. Entonces su rango ya no es tres. Pero como hay al menos un menor de orden dos distinto de cero, su rango es dos:

$$|A|=\begin{vmatrix}1&3\\ -1&-1\\ \end{vmatrix}=-1-(-3)=-1+3=2\neq0\Rightarrow r(A)=2$$

Caso 7

$A$ es una matriz de orden $3\times4$: $A=\begin{pmatrix}a_{11}&a_{12}&a_{13}&a_{14}\\ a_{21}&a_{22}&a_{23}&a_{24}\\ a_{31}&a_{32}&a_{31}&a_{34}\\ \end{pmatrix}$.

En este caso, la matriz $A$ tiene cuatro menores de orden tres:

$$\begin{vmatrix}a_{11}&a_{12}&a_{13}\\ a_{21}&a_{22}&a_{23}\\ a_{31}&a_{32}&a_{31}\\ \end{vmatrix}\quad;\quad \begin{vmatrix}a_{11}&a_{12}&a_{14}\\ a_{21}&a_{22}&a_{24}\\ a_{31}&a_{32}&a_{34}\\ \end{vmatrix}\quad;\quad \begin{vmatrix}a_{11}&a_{13}&a_{14}\\ a_{21}&a_{23}&a_{24}\\ a_{31}&a_{33}&a_{34}\\ \end{vmatrix}\quad;\quad \begin{vmatrix}a_{12}&a_{13}&a_{14}\\ a_{22}&a_{23}&a_{24}\\ a_{32}&a_{33}&a_{34}\\ \end{vmatrix}$$

Si alguno de ellos es distinto de cero, $r(A)=3$. Si todos son cero, entonces $r(A)\leq2$.

Por ejemplo, consideremos la matriz $A=\begin{pmatrix}1&2&-1&-2\\ 3&0&1&-4\\ 1&-1&1&-1\\ \end{pmatrix}$.

Puede comprobarse que todos los menores de orden tres son nulos:

$$\begin{vmatrix}1&2&-1\\ 3&0&1\\ 1&-1&1\\ \end{vmatrix} = \begin{vmatrix}1&2&-2\\ 3&0&-4\\ 1&-1&-1\\ \end{vmatrix} = \begin{vmatrix}1&-1&-2\\ 3&1&-4\\ 1&1&-1\\ \end{vmatrix} = \begin{vmatrix}2&-1&-2\\ 0&1&-4\\ -1&1&-1\\ \end{vmatrix} = 0$$

Como $\begin{vmatrix}1&2\\ 3&0\\ \end{vmatrix}=0-6=-6\neq0$, se tiene que $r(A)=2$.

Caso 8

$A$ es una matriz de orden $4\times3$. Entonces, como su traspuesta es de orden $3\times4$, por la propiedad d), $r(A)=r\left(A^t\right)$, y se procede como en el caso anterior.

Caso 9

$A$ es una matriz de orden $3\times m$, con $m>4$. En este caso se procede como en el caso 7, lo que ocurre es que habrá más menores de orden tres.

Caso 10

$A$ es una matriz de orden $n\times3$, con $n>4$. En este caso se procede como en el caso 8.

Se han analizado especialmente estos casos porque se usarán para la resolución de muchos sistemas de ecuaciones lineales que aparecen con frecuencia en los exámenes.

Método general para hallar el rango de una matriz a partir de sus menores

Ya hemos visto anteriormente varios ejemplos de cálculo del rango de una matriz. La mejor forma de explicar el método general es hacerlo con otro ejemplo.

Supongamos que queremos hallar el rango de $A=\begin{pmatrix}-1&3&0&1&2\\ 0&5&1&2&3\\ -3&-1&-2&-1&0\\ 3&11&4&5&6\\ \end{pmatrix}$. Observa que el orden de la matriz $A$ es $4\times5$, con lo que $r(A)\leq4$.

En primer lugar, se busca un menor de orden dos no nulo. Por ejemplo, $\begin{vmatrix}-1&0\\ 0&1 \\ \end{vmatrix}=-1\neq0$. Esto asegura que el rango de $A$ ya es, al menos, dos. Obsérvese que el menor está formado por las filas 1 y 2, y las columnas 1 y 3. Ahora, con la tercera fila, calculamos todos los menores de orden tres que contengan al menor anterior. Son los siguientes:

$$\begin{vmatrix}-1&3&0\\ 0&5&1\\ -3&-1&-2\\ \end{vmatrix}=0\quad;\quad \begin{vmatrix}-1&0&1\\ 0&1&2\\ -3&-2&-1\\ \end{vmatrix}=0\quad;\quad \begin{vmatrix}-1&0&2\\ 0&1&3\\ -3&-2&0\\ \end{vmatrix}=0$$

Ahora hacemos los mismo que antes, pero con la cuarta fila. Los tres menores de orden 3 que así se obtienen son también iguales a cero (¡compruébese!).

Este método se conoce con el nombre de orlar un menor con menores de orden una unidad superior. Pues bien, es posible demostrar que, si todos los menores obtenidos de este modo son cero, el resto también lo son.

De aquí deducimos que $r(A)=2$ (mayor orden de los menores no nulos de $A$).

Si algún menor de orden tres fuese distinto de cero, el rango de la matriz sería al menos 3 y procederíamos a orlar con los de orden 4. Este método se repite sucesivamente hasta obtener el rango de la matriz $A$ como el mayor orden de los menores no nulos de $A$.

Normalmente, se comienza a orlar con el primer menor de orden dos disponible, caso de que este sea distinto de cero. En el ejemplo anterior, este menor es el formado por las dos primeras filas y las dos primeras columnas, es decir, el menor $\begin{vmatrix}-1&3\\ 0&5 \\ \end{vmatrix}=-5\neq0$. Ahora se puede comprobar que los seis menores de orden tres que lo contienen son iguales a cero (al igual que lo que ocurría anteriormente), con lo que el rango de la matriz es dos.

No será habitual que nos pidan calcular el rango de una matriz de orden superior a $4\times4$, como en el caso del ejemplo anterior. Para matrices de orden $4\times4$. deberemos de saber calcular determinantes de orden cuatro, pero eso lo dejaremos para otro momento.

Rango de matrices dependientes de un parámetro

Por último, haremos un par de ejemplos de cálculo del rango de matrices dependiendo de un parámetro.

Ejemplo 1

Calcular el rango de la matriz $B=\begin{pmatrix}t&t&0\\ 2&t+1&t-1\\ 2t+1&0&-t-3\\ \end{pmatrix}$, en función del parámetro $t$.

Como esta matriz es cuadrada de orden tres, tendrá rango tres si su determinante es distinto de cero. En caso contrario su rango será menor que tres. Pero todo ello dependerá de los valores que tome el parámetro $t$.

El determinante de la matriz $B$ es:

$$|B|=\begin{vmatrix}t&t&0\\ 2&t+1&t-1\\ 2t+1&0&-t-3\\ \end{vmatrix}=t\left( {t + 1} \right)\left( { – t – 3} \right) + t\left( {t – 1} \right)\left( {2t + 1} \right) – 2t\left( { – t – 3} \right)=$$

$$=t\left( {\left( {t + 1} \right)\left( { – t – 3} \right) + \left( {t – 1} \right)\left( {2t + 1} \right) – 2\left( { – t – 3} \right)} \right)=$$

$$=t\left( { – {t^2} – 4t – 3 + 2{t^2} – t – 1 + 2t + 6} \right) = t\left( {{t^2} – 3t + 2} \right)$$

Ahora podemos hallar los valores de $t$ para los cuales el determinante de $B$ es cero:

$$|B| = 0 \Leftrightarrow t(t^2 – 3t + 2) = 0 \Leftrightarrow \begin{cases} t = 0\\ t^2 – 3t + 2 = 0 \end{cases}$$

Pero

$${t^2} – 3t + 2 = 0 \Leftrightarrow t = \frac{{ – \left( { – 3} \right) \pm \sqrt {{{\left( { – 3} \right)}^2} – 4 \cdot 1 \cdot 2} }}{{2 \cdot 1}} = \frac{{3 \pm \sqrt {9 – 8} }}{2} = \frac{{3 \pm 1}}{2} = \begin{cases} t = 2\\ t = 1 \end{cases}$$

Resumiendo, $|B|=0$ si $t=0$, o $t=1$, o bien $t=2$.

De aquí ya podemos afirmar que si $t\neq0$, $t\neq1$ y $t\neq2$, entonces $|B|\neq0$, con lo que $r(B)=3$.

Si $t=0$, $B=\begin{pmatrix}0&0&0\\ 2&1&-1\\ 1&0&3\\ \end{pmatrix}$. Si $t=1$, $B=\begin{pmatrix}1&1&0\\ 2&2&0\\ 3&0&-4\\ \end{pmatrix}$. Si $t=2$, $B=\begin{pmatrix}2&2&0\\ 2&3&1\\ 5&0&-5\\ \end{pmatrix}$

En cualquiera de los casos se tiene que $r(B)=2$, porque en cada uno de los tres casos se pueden encontrar menores de orden dos distintos de cero.

Ejemplo 2

Se trataría de estudiar el rango de la matriz $A=\begin{pmatrix}a&1&3&0\\ 1&a&2&1\\ 2&2a&5&a\\ \end{pmatrix}$, según los valores del parámetro $a$.

Un menor de orden dos distinto de cero es $\begin{vmatrix}3&0\\2&1 \end{vmatrix}=3\neq0$. Esto quiere decir que el rango de $A$ al menos dos.

El menor anterior contiene dos menores de orden tres:

$$\begin{vmatrix}a&3&0\\ 1&2&1\\ 2&5&a \end{vmatrix}=2a^2-8a+6\quad;\quad \begin{vmatrix}1&3&0\\ a&2&1\\ 2a&5&a \end{vmatrix}=-3a^2+8a-5$$

Si ambos fueran igual a cero, el rango de la matriz $A$ no sería igual a tres, con lo que $r(A)=2$. Y si alguno de ellos fuera distinto de cero, entonces $r(A)=3$. Pero eso dependerá de los valores del parámetro $a$. Igualemos a cero ambos y veamos qué ocurre.

$$\begin{vmatrix}a&3&0\\ 1&2&1\\ 2&5&a \end{vmatrix}=2a^2-8a+6=0\Leftrightarrow a=\frac{-(-8)\pm\sqrt{(-8)^2-4\cdot2\cdot6}}{2\cdot2}=$$

$$=\frac{-(-8)\pm\sqrt{16}}{4}=\frac{-(-8)\pm4}{4}=\begin{cases}a_1=3\\a_2=1\end{cases}$$

$$\begin{vmatrix}1&3&0\\ a&2&1\\ 2a&5&a \end{vmatrix}=-3a^2+8a-5=0\Leftrightarrow a=\frac{-8\pm\sqrt{8^2-4\cdot(-3)\cdot(-5)}}{2\cdot(-3)}=$$

$$=\frac{-8\pm\sqrt{4}}{-6}=\frac{-8\pm2}{-6}=\begin{cases}a_1=1\\a_2=\frac{5}{3}\end{cases}$$

De lo anterior se desprende que él único valor común para el que los dos menores de orden tres es igual a cero, es $a=1$. Si $a$ toma cualquier otro valor, alguno de ellos será distinto de cero. Por tanto, podemos concluir lo siguiente.

Si $a=1$, $r(A)=2$. Y si $a\neq1$, $r(A)=3$.

---

Puedes ver y descargar este artículo en formato pdf aquí.