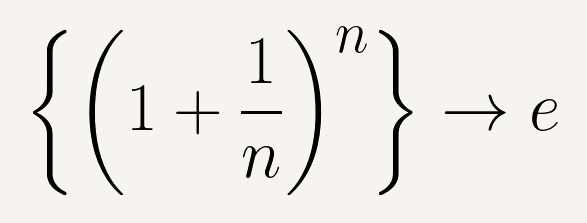Archivos mensuales: enero 2024

El número e

Publicado el por

Si se introduce el número \(\text{e}\), uno de los números reales más importantes, a la manera matemáticamente formal, quizás dé un poco de miedo. Así que lo haré de una forma, si no divertida, al menos curiosa. Para ello prácticamente transcribiré parte de un libro cuyo título es Matemática, ¿estás ahí?«. Su autor es Adrián Paenza. Adrián es doctor en Matemática, profesor y también un reconocido periodista en los ámbitos deportivo y político. Recomiendo encarecidamente la lectura de su libro.

Pues bien, empecemos.

Supongamos que una persona tiene un capital de \(1\) euro. Y vamos a suponer también que el interés que le pagan anualmente por ese euro es del \(100\,\%\). Es sólo un ejemplo, ya sabemos que no existe ni existirá tal banco, pues se arruinaría antes de empezar. Pero da igual, será un ejemplo que nos servirá. Así que seguid el razonamiento.

Capital: 1 euro

Interés: 100% anual

Si uno hace la inversión en el banco y se va a su casa, ¿cuánto dinero tiene cuando vuelve justo al año? Está claro, como el interés es del \(100\,\%\), al año el señor tiene \(2\) euros: uno que corresponde a su capital y otro que es producto del interés que le pagó el banco.

Capital al cabo de un año: 2 euros

Supongamos ahora que el señor decide poner su dinero no a un año, sino sólo a seis meses. El interés (a lo largo de todo este ejemplo) permanecerá constante: siempre será de un \(100\,\%\). Al cabo de seis meses entonces, el señor ¿cuánto dinero tiene? Está claro que tiene \(1,5\) euros.

Esto es porque como invirtió el mismo capital de \(1\) euro a un interés del \(100\,\%\) pero sólo durante la mitad del año, le corresponde un interés de la mitad de lo que invirtió y, por eso, le corresponden \(0,5\) euros de interés. Es decir, su nuevo capital es de \(1,5\) euros.

Prestad atención porque ahora viene lo bueno. Si ahora el señor decide reinvertir su nuevo capital en el mismo banco, con el mismo interés (\(100\,\%\)) y por otros seis meses para llegar nuevamente al año como antes, ¿cuánto dinero tiene ahora?

Nuevo capital: 1,5 euros

Interés: 100% anual

Plazo que lo deposita: 6 meses

Al finalizar el año tiene:

\[1,5+\frac{1}{2}\cdot1,5=2,25\]

¿Por qué? Porque el capital que tenía a los seis meses iniciales no se toca: \(1,5\) euros. El nuevo interés que cobra es de la mitad del capital, porque el dinero lo pone a un interés del \(100\,\%\) pero sólo por seis meses. Por eso, tiene \(1/2\cdot1,5=0,75\) como nuevo dinero que le aporta el banco como producto de los intereses devengados.

MORALEJA: al señor le conviene (siempre que el banco se lo permita) depositar el dinero en primer lugar a seis meses y luego renovar el plazo fijo a otros seis meses. Si comparamos con lo que le hubiera correspondido en el primer caso, al finalizar el año tenía \(2\) euros. En cambio, reinvirtiendo en la mitad, al cabo de \(365\) días tiene \(2,25\) euros.

Supongamos ahora que el señor coloca el mismo euro que tenía originalmente, pero ahora por cuatro meses. Al cabo de esos cuatro meses, reinvierte el dinero, pero por otros cuatro meses. Y finalmente, hace una última reinversión (siempre con el mismo capital) hasta concluir el año. ¿Cuánto dinero tiene ahora? Veamos.

Al principio del año el señor tiene:

\[1\]

A los cuatro meses (o sea, transcurrido \(1/3\) del año) tiene:

\[1+\frac{1}{3}\]

A los siguientes cuatro meses (ocho desde el comienzo) tiene:

\[\left(1+\frac{1}{3}\right)+\frac{1}{3}\left(1+\frac{1}{3}\right)=\left(1+\frac{1}{3}\right)\left(1+\frac{1}{3}\right)=\left(1+\frac{1}{3}\right)^2\]

Esto sucede porque a los cuatro meses el capital es de \((1+1/3)\) y, al cabo de otros cuatro meses, tendrá el capital más un tercio de ese capital. La cuenta que sigue despues se obtiene de sacar factor comun \((1+1/3)\) en el primer miembro de la igualdad.

Ahora bien: cuando el señor invierte \((1+1/3)^2\) por otros cuatro meses, al llegar justo el fin del año, el señor tendrá el capital \((1+1/3)^2\) más \(1/3\) de ese capital. O sea:

\[\left(1+\frac{1}{3}\right)^2+\frac{1}{3}\left(1+\frac{1}{3}\right)^2=\left(1+\frac{1}{3}\right)^2\left(1+\frac{1}{3}\right)=\left(1+\frac{1}{3}\right)^3=2,370370370\ldots\]

Os habréis apercibido de que ahora nos queda la tentación de hacerlo no sólo cada cuatro meses, sino cada tres meses. Podéis echar la cuenta y obtendréis que, al cabo de un año el señor tendrá:

\[\left(1+\frac{1}{4}\right)^4=2,44140625\ldots\]

Si lo hiciera cada dos meses, tendría que reinvertir su dinero seis veces al año:

\[\left(1+\frac{1}{6}\right)^6=2,521626372\ldots\]

Si lo hicera una vez al mes, reinvirtiría doce veces por año:

\[\left(1+\frac{1}{12}\right)^{12}=2,61303529\ldots\]

Como podéis ver, al señor le conviene poner su diner a plazo fijo, pero haciéndolo con un plazo cada vez más corto y reinvirtiendo lo que obtiene (siempre con el mismo interés).

Supongamos que el banco le permitiera al señor renovar su plazo diariamente. En este caso, el señor tendría:

\[\left(1+\frac{1}{365}\right)^{365}=2,714567475\ldots\]

Y si lo hiciera una vez por hora, como en el año hay \(8760\) horas, tendría:

\[\left(1+\frac{1}{8760}\right)^{8760}=2,718126664\ldots\]

Y si se le permitiera hacerlo una vez por minuto, como en el año hay \(525600\) minutos, su capital resultaría ser:

\[\left(1+\frac{1}{525600}\right)^{525600}=2,718279243\ldots\]

Y, por último, supongamos que le permitieran hacerlo una vez por segundo. En este caso, como en el año hay \(31536000\) segundos el capital que tendría al cabo de un año sería:

\[\left(1+\frac{1}{31536000}\right)^{31536000}=2,718281785\ldots\]

MORALEJA: si bien uno advierte que el dinero al finalizar el año es cada vez mayor, el dinero que uno tiene al final no aumenta indiscriminadamente.

Hagamos un resumen de la lista que acabamos de escribir, en la que aparezca las veces al año que renueva su capital y su capital final:

1 vez al año – 2

2 veces al año – 2,25

3 veces al año (cuatrimestral) – 2,37037037…

4 veces al año (trimestral) – 2,44140625…

6 veces al año (bimestral) – 2,521626372…

12 veces al año (mensual) – 2,61303529…

365 veces al año (diario) – 2,714567475…

8.760 veces al año (por hora) – 2,718126664…

525.600 veces al año (una vez por minuto) – 2,718279243…

31.536.000 veces al año (una vez por segundo) – 2,718281785…

Lo que es muy interesante es que estos números, si bien crecen cada vez que el interés se cobra más frecuentemente, no lo hacen en forma ni arbitraria ni desbocada. Al contrario: tienen un tope, están acotados. Y la cota superior (es decir, si uno pudiera imaginariamente estar renovándolo a cada instante) es lo que se conoce como el número \(\text{e}\) (que es la base de los logaritmos naturales o neperianos). No sólo es una cota superior, sino que es el número al cual se está acercando cada vez más la sucesión que estamos generando al modificar los plazos de inversión.

El número \(\text{e}\) es un número irracional, cuyas primeras cifras decimales son:

\[\text{e}=2,718281828…\]

El número \(\text{e}\) es uno de los números más importantes de la vida cotidiana, aunque su relevancia está generalmente escondida para el gran público. Habría que divulgar mucho más sobre él. Por ahora, nos contentamos con celebrar su curiosa aparición en este escenario, mostrándolo como el límite (y también la cota superior) del crecimiento de un capital de \(1\) euro a un interés del \(100\,\%\) anual y renovado periódicamente.

Una integral racional

Publicado el por

Vamos a calcular una primitiva de la función \(f(x)=\dfrac{1}{x^2-a^2}\) donde \(a\) es un número real cualquiera distinto de cero. Es decir, se trata de calcular la integral indefinida \(\displaystyle\int{\frac{1}{x^2-a^2}dx}\). Para ello vamos a descomponer en dos fracciones simples la fracción \(\dfrac{1}{x^2-a^2}\). Como \(x^2-a^2=(x+a)(x-a)\), tenemos:

\[\frac{1}{x^2-a^2}=\frac{E}{x+a}+\frac{F}{x-a}=\frac{E(x-a)+F(x+a)}{(x+a)(x-a)}=\]

\[=\frac{Ex-Ea+Fx+Fa}{x^2-a^2}=\frac{(E+F)x-Ea+Fa}{x^2-a^2}\]

De aquí se deduce, igualando las fracciones algebraicas primera y última, que

\[\begin{cases}E+F=0\\-Ea+Fa=1\end{cases}\Rightarrow\begin{cases}E=-F\\2Fa=1\end{cases}\Rightarrow\begin{cases}E=-\frac{1}{2a}\\F=\frac{1}{2a}\end{cases}\]

Es decir:

\[\frac{1}{x^2-a^2}=\frac{-\frac{1}{2a}}{x+a}+\frac{\frac{1}{2a}}{x-a}\]

Por tanto:

\[\int{\frac{1}{x^2-a^2}dx}=\int{\frac{-\frac{1}{2a}}{x+a}dx}+\int{\frac{\frac{1}{2a}}{x-a}dx}=\]

\[=-\frac{1}{2a}\int{\frac{1}{x+a}dx}+\frac{1}{2a}\int{\frac{1}{x-a}dx}=-\frac{1}{2a}\ln|x+a|+\frac{1}{2a}\ln|x-a|+C=\]

\[=\frac{1}{2a}(\ln|x-a|-\ln|x+a|)+C=\frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right|+C\]

O sea:

\[\int{\frac{1}{x^2-a^2}dx}=\frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right|+C\qquad(1)\]

Ejemplo

Calcular \(\displaystyle\int{\frac{2}{4x^2-1}dx}\)

Solución.

\[\int{\frac{2}{4x^2-1}dx}=2\int{\frac{1}{4x^2-1}dx}=2\int{\frac{\frac{1}{4}}{x^2-\frac{1}{4}}dx}=\]

\[=2\cdot\frac{1}{4}\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}=\frac{1}{2}\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}\]

La integral \(\displaystyle\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}\) es del tipo \(\displaystyle\int{\frac{1}{x^2-a^2}dx}\) con \(a=\dfrac{1}{2}\). Por tanto, usando la fórmula \((1)\):

\[\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}=\frac{1}{2\cdot\frac{1}{2}}\ln\left|\frac{x-\frac{1}{2}}{x+\frac{1}{2}}\right|+C=\ln\left|\frac{2x-1}{2x+1}\right|+C\]

Entonces:

\[\int{\frac{2}{4x^2-1}dx}=\frac{1}{2}\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}=\frac{1}{2}\ln\left|\frac{2x-1}{2x+1}\right|+C\]