Conjuntos
Experimentos aleatorios. Sucesos
Probabilidad
Probabilidad condicionada
Probabilidad total. Teorema de Bayes
Distribución binomial
Distribución normal
Conjuntos
Experimentos aleatorios. Sucesos
Probabilidad
Probabilidad condicionada
Probabilidad total. Teorema de Bayes
Distribución binomial
Distribución normal
Todos los problemas de la humanidad proceden de la incapacidad del hombre para permanecer sentado, en silencio, a solas en una habitación
Si se introduce el número $\text{e}$, uno de los números reales más importantes, a la manera matemáticamente formal, quizás dé un poco de miedo. Así que lo haré de una forma, si no divertida, al menos curiosa. Para ello prácticamente transcribiré parte de un libro cuyo título es Matemática, ¿estás ahí?. Su autor es Adrián Paenza. Adrián es doctor en Matemática, profesor y también un reconocido periodista en los ámbitos deportivo y político. Recomiendo encarecidamente la lectura de su libro.
Pues bien, empecemos.
Supongamos que una persona tiene un capital de \(1\) euro. Y vamos a suponer también que el interés que le pagan anualmente por ese euro es del \(100\,\%\). Es sólo un ejemplo, ya sabemos que no existe ni existirá tal banco, pues se arruinaría antes de empezar. Pero da igual, será un ejemplo que nos servirá. Así que seguid el razonamiento.
Capital: 1 euro
Interés: 100% anual
Si uno hace la inversión en el banco y se va a su casa, ¿cuánto dinero tiene cuando vuelve justo al año? Está claro, como el interés es del \(100\,\%\), al año el señor tiene \(2\) euros: uno que corresponde a su capital y otro que es producto del interés que le pagó el banco.
Capital al cabo de un año: 2 euros
Supongamos ahora que el señor decide poner su dinero no a un año, sino sólo a seis meses. El interés (a lo largo de todo este ejemplo) permanecerá constante: siempre será de un \(100\,\%\). Al cabo de seis meses entonces, el señor ¿cuánto dinero tiene? Está claro que tiene \(1,5\) euros.
Esto es porque como invirtió el mismo capital de \(1\) euro a un interés del \(100\,\%\) pero sólo durante la mitad del año, le corresponde un interés de la mitad de lo que invirtió y, por eso, le corresponden \(0,5\) euros de interés. Es decir, su nuevo capital es de \(1,5\) euros.
Prestad atención porque ahora viene lo bueno. Si ahora el señor decide reinvertir su nuevo capital en el mismo banco, con el mismo interés (\(100\,\%\)) y por otros seis meses para llegar nuevamente al año como antes, ¿cuánto dinero tiene ahora?
Nuevo capital: 1,5 euros
Interés: 100% anual
Plazo que lo deposita: 6 meses
Al finalizar el año tiene:
\[1,5+\frac{1}{2}\cdot1,5=2,25\]
¿Por qué? Porque el capital que tenía a los seis meses iniciales no se toca: \(1,5\) euros. El nuevo interés que cobra es de la mitad del capital, porque el dinero lo pone a un interés del \(100\,\%\) pero sólo por seis meses. Por eso, tiene \(1/2\cdot1,5=0,75\) como nuevo dinero que le aporta el banco como producto de los intereses devengados.
MORALEJA: al señor le conviene (siempre que el banco se lo permita) depositar el dinero en primer lugar a seis meses y luego renovar el plazo fijo a otros seis meses. Si comparamos con lo que le hubiera correspondido en el primer caso, al finalizar el año tenía \(2\) euros. En cambio, reinvirtiendo en la mitad, al cabo de \(365\) días tiene \(2,25\) euros.
Supongamos ahora que el señor coloca el mismo euro que tenía originalmente, pero ahora por cuatro meses. Al cabo de esos cuatro meses, reinvierte el dinero, pero por otros cuatro meses. Y finalmente, hace una última reinversión (siempre con el mismo capital) hasta concluir el año. ¿Cuánto dinero tiene ahora? Veamos.
Al principio del año el señor tiene:
\[1\]
A los cuatro meses (o sea, transcurrido \(1/3\) del año) tiene:
\[1+\frac{1}{3}\]
A los siguientes cuatro meses (ocho desde el comienzo) tiene:
\[\left(1+\frac{1}{3}\right)+\frac{1}{3}\left(1+\frac{1}{3}\right)=\left(1+\frac{1}{3}\right)\left(1+\frac{1}{3}\right)=\left(1+\frac{1}{3}\right)^2\]
Esto sucede porque a los cuatro meses el capital es de \((1+1/3)\) y, al cabo de otros cuatro meses, tendrá el capital más un tercio de ese capital. La cuenta que sigue despues se obtiene de sacar factor comun \((1+1/3)\) en el primer miembro de la igualdad.
Ahora bien: cuando el señor invierte \((1+1/3)^2\) por otros cuatro meses, al llegar justo el fin del año, el señor tendrá el capital \((1+1/3)^2\) más \(1/3\) de ese capital. O sea:
\[\left(1+\frac{1}{3}\right)^2+\frac{1}{3}\left(1+\frac{1}{3}\right)^2=\left(1+\frac{1}{3}\right)^2\left(1+\frac{1}{3}\right)=\left(1+\frac{1}{3}\right)^3=2,370370370\ldots\]
Os habréis apercibido de que ahora nos queda la tentación de hacerlo no sólo cada cuatro meses, sino cada tres meses. Podéis echar la cuenta y obtendréis que, al cabo de un año el señor tendrá:
\[\left(1+\frac{1}{4}\right)^4=2,44140625\ldots\]
Si lo hiciera cada dos meses, tendría que reinvertir su dinero seis veces al año:
\[\left(1+\frac{1}{6}\right)^6=2,521626372\ldots\]
Si lo hicera una vez al mes, reinvirtiría doce veces por año:
\[\left(1+\frac{1}{12}\right)^{12}=2,61303529\ldots\]
Como podéis ver, al señor le conviene poner su dinero a plazo fijo, pero haciéndolo con un plazo cada vez más corto y reinvirtiendo lo que obtiene (siempre con el mismo interés).
Supongamos que el banco le permitiera al señor renovar su plazo diariamente. En este caso, el señor tendría:
\[\left(1+\frac{1}{365}\right)^{365}=2,714567475\ldots\]
Y si lo hiciera una vez por hora, como en el año hay \(8760\) horas, tendría:
\[\left(1+\frac{1}{8760}\right)^{8760}=2,718126664\ldots\]
Y si se le permitiera hacerlo una vez por minuto, como en el año hay \(525600\) minutos, su capital resultaría ser:
\[\left(1+\frac{1}{525600}\right)^{525600}=2,718279243\ldots\]
Y, por último, supongamos que le permitieran hacerlo una vez por segundo. En este caso, como en el año hay \(31536000\) segundos el capital que tendría al cabo de un año sería:
\[\left(1+\frac{1}{31536000}\right)^{31536000}=2,718281785\ldots\]
MORALEJA: si bien uno advierte que el dinero al finalizar el año es cada vez mayor, el dinero que uno tiene al final no aumenta indiscriminadamente.
Hagamos un resumen de la lista que acabamos de escribir, en la que aparezca las veces al año que renueva su capital y su capital final:
1 vez al año – 2
2 veces al año – 2,25
3 veces al año (cuatrimestral) – 2,37037037…
4 veces al año (trimestral) – 2,44140625…
6 veces al año (bimestral) – 2,521626372…
12 veces al año (mensual) – 2,61303529…
365 veces al año (diario) – 2,714567475…
8.760 veces al año (por hora) – 2,718126664…
525.600 veces al año (una vez por minuto) – 2,718279243…
31.536.000 veces al año (una vez por segundo) – 2,718281785…
Lo que es muy interesante es que estos números, si bien crecen cada vez que el interés se cobra más frecuentemente, no lo hacen en forma ni arbitraria ni desbocada. Al contrario: tienen un tope, están acotados. Y la cota superior (es decir, si uno pudiera imaginariamente estar renovándolo a cada instante) es lo que se conoce como el número \(\text{e}\) (que es la base de los logaritmos naturales o neperianos). No sólo es una cota superior, sino que es el número al cual se está acercando cada vez más la sucesión que estamos generando al modificar los plazos de inversión.
El número \(\text{e}\) es un número irracional, cuyas primeras cifras decimales son:
\[\text{e}=2,718281828…\]
El número \(\text{e}\) es uno de los números más importantes de la vida cotidiana, aunque su relevancia está generalmente escondida para el gran público. Habría que divulgar mucho más sobre él. Por ahora, nos contentamos con celebrar su curiosa aparición en este escenario, mostrándolo como el límite (y también la cota superior) del crecimiento de un capital de \(1\) euro a un interés del \(100\,\%\) anual y renovado periódicamente.
Conviene aprender hasta del enemigo
Vamos a calcular una primitiva de la función \(f(x)=\dfrac{1}{x^2-a^2}\) donde \(a\) es un número real cualquiera distinto de cero. Es decir, se trata de calcular la integral indefinida \(\displaystyle\int{\frac{1}{x^2-a^2}dx}\). Para ello vamos a descomponer en dos fracciones simples la fracción \(\dfrac{1}{x^2-a^2}\). Como \(x^2-a^2=(x+a)(x-a)\), tenemos:
\[\frac{1}{x^2-a^2}=\frac{E}{x+a}+\frac{F}{x-a}=\frac{E(x-a)+F(x+a)}{(x+a)(x-a)}=\]
\[=\frac{Ex-Ea+Fx+Fa}{x^2-a^2}=\frac{(E+F)x-Ea+Fa}{x^2-a^2}\]
De aquí se deduce, igualando las fracciones algebraicas primera y última, que
\[\begin{cases}E+F=0\\-Ea+Fa=1\end{cases}\Rightarrow\begin{cases}E=-F\\2Fa=1\end{cases}\Rightarrow\begin{cases}E=-\frac{1}{2a}\\F=\frac{1}{2a}\end{cases}\]
Es decir:
\[\frac{1}{x^2-a^2}=\frac{-\frac{1}{2a}}{x+a}+\frac{\frac{1}{2a}}{x-a}\]
Por tanto:
\[\int{\frac{1}{x^2-a^2}dx}=\int{\frac{-\frac{1}{2a}}{x+a}dx}+\int{\frac{\frac{1}{2a}}{x-a}dx}=\]
\[=-\frac{1}{2a}\int{\frac{1}{x+a}dx}+\frac{1}{2a}\int{\frac{1}{x-a}dx}=-\frac{1}{2a}\ln|x+a|+\frac{1}{2a}\ln|x-a|+C=\]
\[=\frac{1}{2a}(\ln|x-a|-\ln|x+a|)+C=\frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right|+C\]
O sea:
\[\int{\frac{1}{x^2-a^2}dx}=\frac{1}{2a}\ln\left|\frac{x-a}{x+a}\right|+C\qquad(1)\]
Calcular \(\displaystyle\int{\frac{2}{4x^2-1}dx}\)
Solución.
\[\int{\frac{2}{4x^2-1}dx}=2\int{\frac{1}{4x^2-1}dx}=2\int{\frac{\frac{1}{4}}{x^2-\frac{1}{4}}dx}=\]
\[=2\cdot\frac{1}{4}\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}=\frac{1}{2}\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}\]
La integral \(\displaystyle\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}\) es del tipo \(\displaystyle\int{\frac{1}{x^2-a^2}dx}\) con \(a=\dfrac{1}{2}\). Por tanto, usando la fórmula \((1)\):
\[\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}=\frac{1}{2\cdot\frac{1}{2}}\ln\left|\frac{x-\frac{1}{2}}{x+\frac{1}{2}}\right|+C=\ln\left|\frac{2x-1}{2x+1}\right|+C\]
Entonces:
\[\int{\frac{2}{4x^2-1}dx}=\frac{1}{2}\int{\frac{1}{x^2-\left(\frac{1}{2}\right)^2}dx}=\frac{1}{2}\ln\left|\frac{2x-1}{2x+1}\right|+C\]
Todo lo que no se comprende, envenena
En la entrada anterior sobre integrales indefinidas se obtuvieron las siguientes:
\[\int{\cos^2x\,dx}=\frac{x+\text{sen}\,x\cos x}{2}+C\]
\[\int{\text{sen}^2x\,dx}=\frac{x-\text{sen}\,x\cos x}{2}+C\]
\[\int{x\cos x\,dx}=x\,\text{sen}\,x+\cos x+C\]
\[\int{x\,\text{sen}\,x\,dx}=-x\cos x+\text{sen}\,x+C\]
\[\int{\text{sen}\,x\cos x\,dx}=\frac{\text{sen}^2x}{2}+C=-\frac{\cos^2x}{2}+C\]
Vamos a calcular un par de ellas más. Para ello utilizaremos algunas de las fórmulas anteriores.
\[\int{x\,\text{sen}^2x\,dx}=\begin{bmatrix}u=x&\text{;}&du=dx\\dv=\text{sen}^2x\,dx&\text{;}&v=\frac{1}{2}(x-\text{sen}\,x\cos x)\end{bmatrix}=\]
\[=\frac{1}{2}x(x-\text{sen}\,x\cos x)-\frac{1}{2}\int{(x-\text{sen}\,x\cos x)\,dx}=\]
\[=\frac{1}{2}x^2-\frac{1}{2}x\,\text{sen}\,x\cos x-\frac{1}{2}\,\frac{x^2}{2}+\frac{1}{2}\,\frac{\text{sen}^2x}{2}+C=\]
\[=\frac{1}{4}x^2-\frac{1}{2}x\,\text{sen}\,x\cos x+\frac{1}{4}\text{sen}^2x+C\]
\[\int{x\cos^2x\,dx}=\int{x(1-\text{sen}^2x)\,dx}=\int{x\,dx}-\int{x\,\text{sen}^2x\,dx}=\]
\[=\frac{1}{2}x^2-\left(\frac{1}{4}x^2-\frac{1}{2}x\,\text{sen}\,x\cos x+\frac{1}{4}\text{sen}^2x+C\right)=\]
\[=\frac{1}{4}x^2+\frac{1}{2}x\,\text{sen}\,x\cos x-\frac{1}{4}\text{sen}^2x+C\]
Si introduces la expresión x*(sin(x))^2 en WolframAlpha obtienes la integral indefinida:
\[\int{x\,\text{sen}^2x\,dx}=\frac{1}{8}\left(2x(x-\text{sen}\,2x)-\cos2x\right)+C\]
que es equivalente a la obtenida anterioremente ya que
\[\frac{1}{8}\left(2x(x-\text{sen}\,2x)-\cos2x\right)=\frac{1}{8}(2x^2-2x\,\text{sen}\,2x-\cos2x)=\]
\[=\frac{1}{4}x^2-\frac{1}{4}x\,2\,\text{sen}\,x\cos x-\frac{1}{8}(\cos^2x-\text{sen}^2x)=\]
\[=\frac{1}{4}x^2-\frac{1}{2}x\,\text{sen}\,x\cos x-\frac{1}{8}(1-2\,\text{sen}^2x)=\]
\[=\frac{1}{4}x^2-\frac{1}{2}x\,\text{sen}\,x\cos x+\frac{1}{4}\text{sen}^2x-\frac{1}{8}\]
El siguiente ejercicio se ha propuesto en el examen de EvAU de Matemáticas II (convocatoria de junio de 2023).
Sean las matrices $X = \left({\begin{array}{c}a&b\\ c&0 \end{array}} \right)$, con $a,\,b\in\mathbb{R}$, $A = \left( {\begin{array}{c} 2&1\\ 4&2 \end{array}} \right)$, $B = \left( {\begin{array}{c} 1&0\\ 2&0 \end{array}} \right)$.
a) Determina las condiciones que tienen que cumplir los valores $a$, $b$, $c$ para que $A\cdot X=B$.
b) Si además queremos que $X$ sea simétrica, ¿qué se debe cumplir? ¿Cómo es la matriz $X$ resultante?
a) $A\cdot X=\left( {\begin{array}{c} 2&1\\ 4&2 \end{array}} \right)\cdot\left( {\begin{array}{c} a&b\\ c&0 \end{array}} \right)=\left( {\begin{array}{c} 2a+c&2b\\ 4a+2c&4b \end{array}} \right)$. Entonces, para que $A\cdot X=B$, se ha de cumplir que
$$\left( {\begin{array}{c} 2a+c&2b\\ 4a+2c&4b \end{array}} \right)=\left( {\begin{array}{c} 1&0\\ 2&0 \end{array}} \right)$$
De aquí se deduce, por un lado, que $2a+c=1$ y $4a+2c=2$, que son ecuaciones equivalentes, ya que la segunda es el doble de la primera. Despejando $c$ de la primera ecuación, tenemos que $c=1-2a$. Por otro lado, se tiene que $2b=0$ y que $4b=0$. O sea, que $b=0$. Por tanto, las condiciones que tienen que cumplir los valores $a$, $b$, $c$ para que $A\cdot X=B$ son $c=1-2a,\ b=0$. De este modo, para que $A\cdot X=B$, debe ser
$$X=\left( {\begin{array}{c} a&0\\ 1-2a&0 \end{array}} \right)$$
b) $X=X^t \Leftrightarrow \left( {\begin{array}{c} a&0\\ 1-2a&0 \end{array}} \right)=\left( {\begin{array}{c} a&1-2a\\ 0&0 \end{array}} \right) \Leftrightarrow 1-2a=0 \Leftrightarrow a=\dfrac{1}{2}$.
Por tanto, la matriz resultante será de la forma
$$X=\left( {\begin{array}{c} \dfrac{1}{2}&0\\ 0&0 \end{array}} \right)$$
Sea un proyectil lanzado verticalmente desde el suelo a una velocidad de \(45\) metros por segundo. Prescindiendo del rozamiento, se supone que solamente actúa la gravedad, por lo que el proyectil se mueve en línea recta. Sea \(f(t)\) la altura en metros que alcanza el proyectil \(t\) segundos después del lanzamiento. Si la fuerza de la gravedad no actuara en él, el proyectil continuaría subiendo a velocidad constante, recorriendo una distancia de \(45\) metros cada segundo, y en el tiempo \(t\) se tendría \(f(t)=45t\). Pero a causa de la gravedad, el proyectil va retardándose hasta que su velocidad llega a valer cero, y a partir de ese momento cae al suelo. Experiencias físicas indican que mientras el proyectil está en movimiento su altura \(f(t)\) viene dada aproximadamente por la fórmula
\[f(t)=45t-5t^2\qquad(1)\]
El término \(-5t^2\) es debido a la influencia de la gravedad. Obsérvese que \(f(t)=0\) cuando \(t=0\) y \(t=9\); o sea, que el proyectil regresa a la tierra después de \(9\) segundos, por lo que la fórmula anterior sólo es válida para \(0\leqslant t\leqslant9\).
El problema a considerar es el siguiente: Determinar la velocidad del proyectil en cada instante de su movimiento. Para poder comprender este problema, hay que precisar lo que se entiende por velocidad en cada instante. Para ello, se introduce la noción de velocidad media durante un intervalo de tiempo, es decir, desde el instante \(t\) al \(t+h\), definiéndola como el cociente:
\[\frac{\text{diferencia de distancias en el intervalo de tiempo}}{\text{intervalo de tiempo}}=\frac{f(t+h)-f(t)}{h}\]
Este cociente, llamado cociente incremental, es un número que se puede calcular siempre que \(t\) y \(t+h\) pertenezcan ambos al intervalo \([0,9]\). El número \(h\) puede ser positivo o negativo, pero no cero. Se dejará fijo \(t\) y se estudiará lo que le ocurre al cociente incremental, cuando se dan a \(h\) valores cada vez menores en valor absoluto.
Por ejemplo, considérese el instante \(t=2\). La distancia recorrida después de \(2\) segundos es:
$$f(2)=90-20=70$$
En el tiempo \(t=2+h\) la distancia recorrida es:
$$f(2+h)=45(2+h)-5(2+h)^2=70+25h-5h^2$$
Por tanto, la velocidad media en el intervalo entre \(t=2\) y \(t=2+h\) es
$$\frac{f(2+h)-f(2)}{h}=\frac{25h-5h^2}{h}=25-5h$$
Tomando valores de \(h\) cada vez más pequeños en valor absoluto, esta velocidad media se acerca más y más a \(25\). Por ejemplo, si \(h=0,1\) la velocidad media es \(24,5\); si \(h=0,001\), es \(24,995\); si \(h=0,00001\), se obtiene el valor \(24,99995\), y cuando \(h=-0,00001\) se obtiene \(25,00005\). Lo importante es que se puede obtener la velocidad media tan próxima a \(25\) como se desee, si más que tomar \(|h|\) suficientemente pequeño. Se describe este hecho diciendo que la velocidad media tiende al límite \(25\) cuando \(h\) tiende a cero. Parece natural llamar al valor de este límite la velocidad instantánea en el instante \(t=2\).
Los mismos cálculos se pueden efectuar para cualquier otro instante. La velocidad media en un intervalo arbitrario entre \(t\) y \(t+h\) está dado por el cociente:
$$\frac{f(t+h)-f(t)}{h}=\frac{(45(t+h)-5(t+h)^2)-(45t-5t^2)}{h}=45-10t-5h$$
Cuando \(h\) tiende a cero, la expresión de la derecha tiende al límite \(45-10t\) que define la velocidad instantánea en el instante \(t\). Designando la velocidad instantánea por \(v(t)\) se tiene
\[v(t)=45-10t\qquad(2)\]
La fórmula \((1)\) del espacio \(f(t)\), define una función \(f\) que indica la altura a que se encuentra el proyectil en cada instante de su movimiento; \(f\) se denomina función posición o ley de espacios. Su dominio es el intervalo cerrado \([0,9]\) y su gráfica es la siguiente:
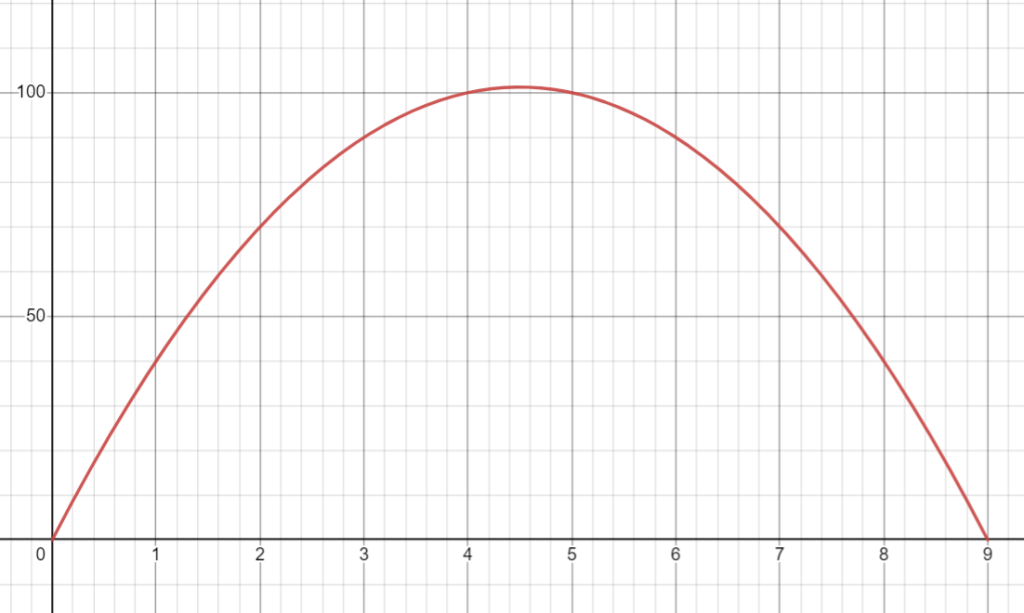
La fórmula \((2)\) de la velocidad \(v(t)\) define una nueva función \(v\) que indica la rapidez con que se mueve el proyectil en cada instante de su movimiento, se denomina función velocidad y su gráfica la tienes a continuación.
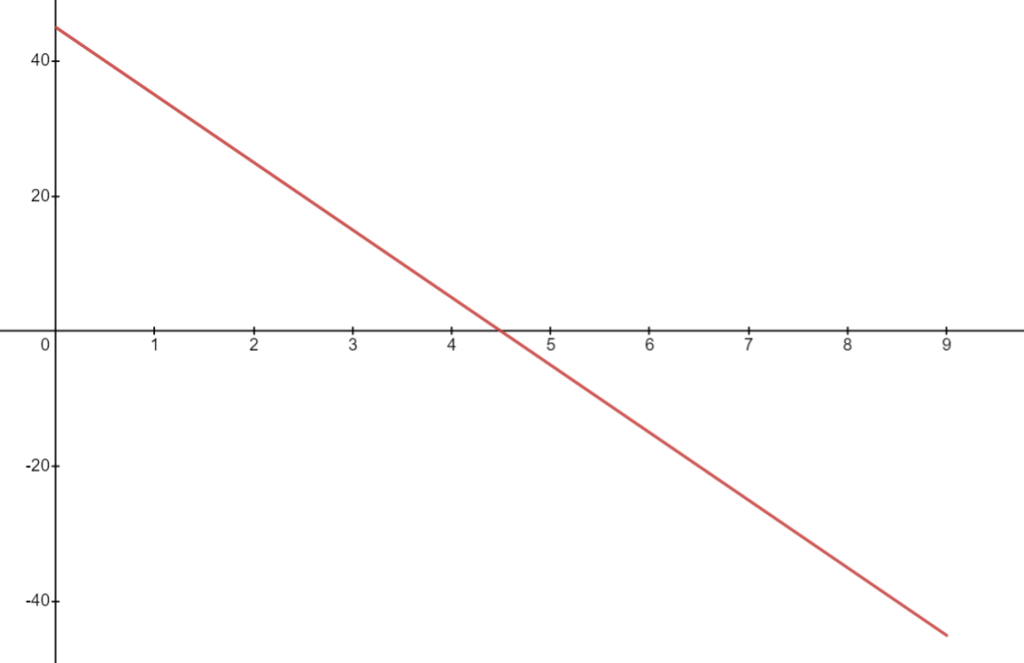
Obsérvese que, al crecer \(t\) de \(0\) a \(9\), \(v(t)\) decrece constantemente de \(v(0)=45\) a \(v(9)=-45\). Para hallar el instante \(t\) en el cual \(v(t)=0\) se resuelve la ecuación \(45-10t=0\) obteniéndose \(t=\frac{9}{2}\). Por tanto, en el punto central del movimiento la influencia de la gravedad reduce la velocidad a cero y el proyectil queda instantáneamente fijo. La altura en este instante es \(f(\frac{9}{2})=101,25\). Si \(t>\frac{9}{2}\), la velocidad es negativa y la altura decrece.
El proceso por el cual se obtiene \(v(t)\) a partir del cociente incremental se denomina «hallar el límite cuando \(h\) tiende a cero», y se expresa simbólicamente como sigue:\[v(t)=\lim_{h\rightarrow0}\frac{f(t+h)-f(t)}{h}\qquad(3)\]
Esta expresión usada para definir la velocidad, en el ejemplo anterior, tiene un sentido más amplio y permite definir la velocidad en movimientos a lo largo de una línea recta, cuando se conozca la función de posición \(f\), y siempre que el cociente incremental tienda a un límite cuando \(h\) tiende a cero.$$\frac{f(x+h)-f(x)}{h}$$
donde el número \(h\) puede ser positivo o negativo (pero no cero), y tal que \(x+h\) pertenezca también a \((a,b)\). El numerador de este cociente mide la variación de la función cuando \(x\) varía de \(x\) a \(x+h\). El cociente representa la variación media de \(f\) en el intervalo que une \(x\) a \(x+h\). Seguidamente se hace tender \(h\) a cero y se estudia lo que le ocurre a ese cociente. Si tiende hacia un cierto valor como límite (y será el mismo, tanto si \(h\) tiende a cero con valores positivos como negativos), entonces ese límite se denomina derivada de \(f\) en \(x\) y se indica por el símbolo \(f'(x)\). Por tanto, la definición formal de \(f'(x)\) puede establecerse del siguiente modo.Definición de derivada.
La derivada \(f'(x)\) está definida por la igualdad$$f'(x)=\lim_{h\to0}\frac{f(x+h)-f(x)}{h}\qquad(4)$$
con tal que el límite exista. El número \(f'(x)\) también se denomina coeficiente de variación de \(f\) en \(x\). Comparando la igualdad \((4)\) con la igualdad \((3)\) se ve que el concepto de velocidad instantánea es simplemente un ejemplo del concepto de derivada. La velocidad \(v(t)\) es igual a la derivada \(f'(t)\) cuando \(f\) es la ley de espacios; lo que frecuentemente se expresa diciendo que la velocidad es la relación entre la variación del espacio y la del tiempo. Ya hemos visto en el apartado anterior que la ley de espacios está dada por la ecuación \(f(t)=45t-t^2\), y su derivada \(f’\) es una nueva función (velocidad) dada por \(f'(t)=45-10t\).En general, el proceso de paso al límite por el que se obtiene \(f'(x)\) a partir de \(f(x)\), abre un camino para obtener una nueva función \(f’\) a partir de una función dada \(f\). Este proceso se denomina derivación, y \(f’\) es la primera derivada de \(f\). Si \(f’\) a su vez está definida en un intervalo abierto, se puede también calcular su primera derivada, indicada por \(f’\,’\) y que es la segunda derivada de \(f\). Análogamente, la derivada \(n\)-sima de \(f\), que se indica por \(f^{(n)}\), se define como la derivada primera de \(f^{(n-1)}\). Convendremos en que \(f^{(0)}=f\), esto es, la derivada de orden cero es la misma función.
En el caso del movimiento rectilíneo, la primera derivada de la velocidad (segunda derivada del espacio) se denomina aceleración. Por ejemplo, para calcular la aceleración en el ejemplo del apartado anterior, se puede utilizar la ecuación \((2)\) para formar el cociente de diferencias$$\frac{v(t+h)-v(t)}{h}=\frac{(45-10(t+h))-(45-10t)}{h}=\frac{-10h}{h}=-10$$
Como este cociente no varía al tender \(h\) a \(0\), se puede considerar que tiende a \(-10\) (puesto que es \(-10\) cuando \(h\) está próximo a \(0\)). Se concluye pues que la aceleración en este problema es constante e igual a \(-10\), lo que indica que la velocidad decrece a una razón de \(10\) metros por segundo cada segundo. En \(9\) segundos el decrecimiento total de la velocidad es \(9\cdot10=90\) metros por segundo, que está de acuerdo con el hecho de que durante los \(9\) segundos de movimiento la velocidad cambie de \(v(0)=45\) a \(v(9)=-45\).$$\frac{f(x+h)-f(x)}{h}=\frac{c-c}{h}=0$$
Puesto que el cociente es \(0\) para todo \(x\), su límite cuando \(h\) tiende a cero, \(f'(x)\), es también \(0\) para todo \(x\). Dicho de otro modo, una función constante tiene derivada nula para todo \(x\).EJEMPLO 2. Derivada de la función lineal. Sea \(f\) una función lineal, por ejemplo \(f(x)=mx+n\) para todo real \(x\). Si \(h\neq0\), tenemos
$$\frac{f(x+h)-f(x)}{h}=\frac{m(x+h)+b-(mx+b)}{h}=\frac{mh}{h}=m$$
Como que el cociente de diferencias no cambia cuando \(h\) tiende a \(0\), resulta que \(f'(x)=m\), para cada \(x\). Así que, la derivada de una función lineal es una función constante.EJEMPLO 3. Derivada de una función potencial de exponente entero positivo. Consideremos el caso \(f(x)=x^n\), siendo \(n\) un entero positivo. El cociente de diferencias es ahora
$$\frac{f(x+h)-f(x)}{h}=\frac{(x+h)^n-x^n}{h}$$
En álgebra elemental se tiene la igualdad (¡compruébese!)$$a^n-b^n=(a-b)\left(b^{n-1}+ab^{n-2}+a^2b^{n-3}+\ldots+a^{n-2}b+a^{n-1}\right)$$
Es conveniente observar que el segundo paréntesis del segundo miembro tiene \(n\) sumandos. Si en la igualdad anterior se toma \(a=x+h\) y \(b=x\), la identidad se transforma en:
$$(x+h)^n-x^n=h\left(x^{n-1}+(x+h)x^{n-2}+(x+h)^2x^{n-3}+\ldots+(x+h)^{n-2}x+(x+h)^{n-1}\right)$$
Si dividimos entre \(h\) los dos miembros de la igualdad tenemos:
$$\frac{(x+h)^n-x^n}{h}=x^{n-1}+(x+h)x^{n-2}+(x+h)^2x^{n-3}+\ldots+(x+h)^{n-2}x+(x+h)^{n-1}$$
Insistimos en que en la suma del segundo miembro hay \(n\) términos. Cuando \(h\) tiende a \(0\) tenemos:
$$\lim_{h\rightarrow0}\frac{(x+h)^n-x^n}{h}=\lim_{h\rightarrow0}\left(x^{n-1}+(x+h)x^{n-2}+(x+h)^2x^{n-3}+\ldots+(x+h)^{n-2}x+(x+h)^{n-1}\right)=$$
$$=x^{n-1}+x\cdot x^{n-2}+x^2\cdot x^{n-3}+\ldots+x^{n-2}\cdot x+x^{n-1}=x^{n-1}+x^{n-1}+x^{n-1}+\ldots n\text{ veces}\ldots+x^{n-1}$$
Por tanto, la suma de los últimos \(n\) términos es \(nx^{n-1}\). En definitiva: \(f'(x)=nx^{n-1}\), para todo \(x\).
EJEMPLO 4. Derivada de la función seno. Sea \(f(x)=\text{sen}\,x\). El cociente de diferencias es
$$\frac{f(x+h)-f(x)}{h}=\frac{\text{sen}(x+h)-\text{sen}\,x}{h}$$
Para transformarlo de modo que haga posible calcular el límite cuando \(h\rightarrow0\), utilizamos la identidad trigonométrica
$$\text{sen}\,A-\text{sen}\,B=2\,\text{sen}\frac{A-B}{2}\cos\frac{A+B}{2}$$
Poniendo \(A=x+h\) y \(B=x\) tenemos
$$\frac{\text{sen}(x+h)-\text{sen}\,x}{h}=\frac{2\,\text{sen}\frac{h}{2}\cos\frac{2x+h}{2}}{h}=\frac{\text{sen}\frac{h}{2}}{\frac{h}{2}}\cos\left(x+\frac{h}{2}\right)$$
Cuando \(h\rightarrow0\), el factor \(\cos\left(x+\frac{h}{2}\right)\rightarrow\cos x\) por la continuidad del coseno. Asimismo, el siguiente límite
$$\lim_{x\rightarrow0}\frac{\text{sen}\,x}{x}=1$$
(ver gráfica de la función \(\frac{\text{sen}\,x}{x}\), la cual tienes a continuación), demuestra que
$$\lim_{h\rightarrow0}\frac{\text{sen}\frac{h}{2}}{\frac{h}{2}}=1$$
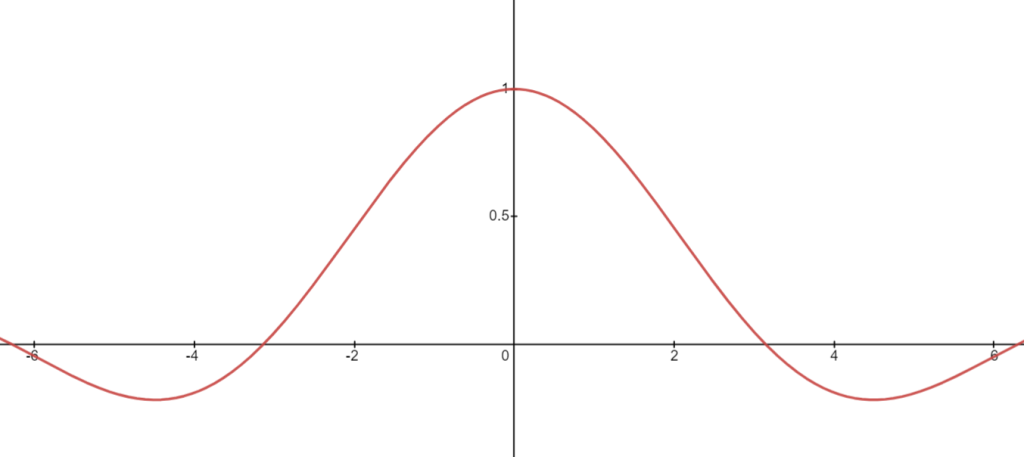
Por lo tanto el cociente de diferencias tiene como límite \(\cos x\) cuando \(h\rightarrow0\). Dicho de otro modo, \(f'(x)=\cos x\) para todo \(x\), es decir, la derivada de la función seno es el coseno.
EJEMPLO 5. Derivada de la función coseno. Sea \(f(x)=\cos x\). Demostraremos que \(f'(x)=-\text{sen}\,x\), esto es, que la derivada de la función coseno es menos la función seno. Hemos de partir ahora de la identidad trigonométrica siguiente:
$$\cos A-\cos B=-2\,\text{sen}\frac{A-B}{2}\text{sen}\frac{A+B}{2}$$
Pongamos \(A=x+h\) y \(B=x\). De manera similar a como se ha procedido en el ejemplo anterior, esto nos conduce a la fórmula
$$\frac{\cos(x+h)-\cos x}{h}=-\frac{2\,\text{sen}\frac{h}{2}\text{sen}\frac{2x+h}{2}}{h}=-\frac{\text{sen}\frac{h}{2}}{\frac{h}{2}}\text{sen}\left(x+\frac{h}{2}\right)$$
La continuidad de la función seno demuestra que \(\text{sen}(x+\frac{h}{2})\rightarrow\text{sen}\,x\) cuando \(h\rightarrow0\). Además, recordemos que \(\displaystyle\lim_{x\rightarrow0}\frac{\text{sen}\,x}{x}=1\). Por tanto \(f'(x)=-\text{sen}\,x\).
EJEMPLO 6. Derivada de la función raíz n-sima. Si \(n\) es un entero positivo, sea \(f(x)=x^{1/n}\) para \(x>0\). El cociente de diferencias para \(f\) es
$$\frac{f(x+h)-f(x)}{h}=\frac{(x+h)^{1/n}-x^{1/n}}{h}$$
Pongamos \(u=(x+h)^{1/n}\) y \(v=x^{1/n}\). Tenemos entonces \(u^n=x+h\) y \(v^n=x\), con lo que \(h=u^n-v^n\), y el cociente de diferencias toma la forma (ver ejemplo 3)
$$\frac{f(x+h)-f(x)}{h}=\frac{u-v}{u^n-v^n}=\frac{1}{u^{n-1}+u^{n-2}v+\ldots+uv^{n-2}+v^{n-1}}$$
La continuidad de la función raíz \(n\)-sima prueba que \(u\rightarrow v\) cuando \(h\rightarrow0\). Por consiguiente, cada término del denominador del miembro de la derecha tiene límite \(v^{n-1}\) cuando \(h\rightarrow0\). En total hay \(n\) términos, con lo que el cociente de diferencias tiene como límite \(\frac{1}{nv^{n-1}}=\frac{v^{1-n}}{n}\). Puesto que \(v=x^{1/n}\), esto demuestra que
$$f'(x)=\frac{x^{(1/n)(1-n)}}{n}=\frac{1}{n}x^{\frac{1}{n}-1}$$
EJEMPLO 7. Continuidad de las funciones que admiten derivadas. Si una función \(f\) tiene derivada en un punto \(x\), es también continua en \(x\). Para demostrarlo, empleamos la identidad
$$f(x+h)=f(x)+h\left(\frac{f(x+h)-f(x)}{h}\right)$$
que es válida para \(h\neq0\). Si hacemos que \(h\rightarrow0\), el cociente de diferencias del segundo miembro tiende a \(f'(x)\) y, puesto que este cociente está multiplicado por un factor que tiende hacia \(0\), el segundo término del segundo miembro tiende a \(0\). Esto demuestra que \(f(x+h)\rightarrow f(x)\) cuando \(h\rightarrow0\), y por tanto que \(f\) es continua en \(x\) (obsérvese que esto es lo mismo que decir, haciendo un adecuado cambio de variable, que \(f(x)\rightarrow f(a)\) cuando \(x\rightarrow a\)).
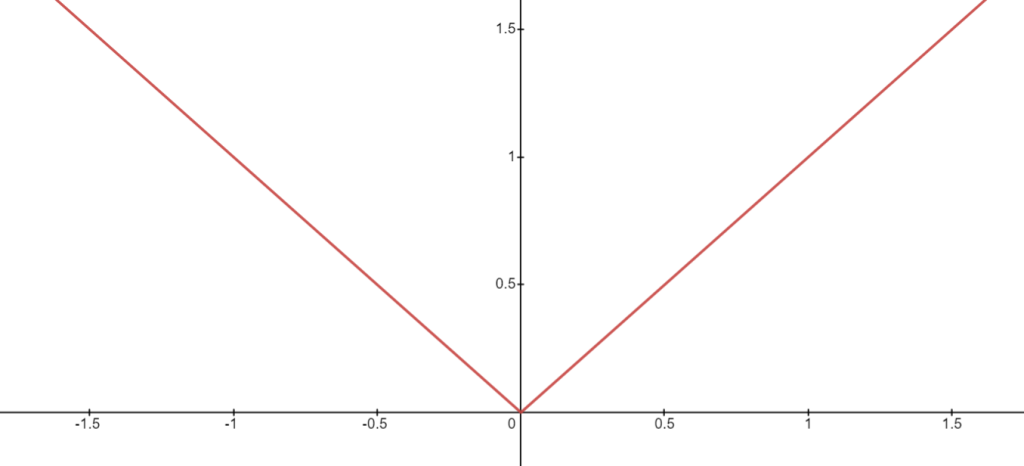
Este último ejemplo proporciona un nuevo procedimiento para probar la continuidad de las funciones. Cada vez que establecemos la existencia de una derivada \(f'(x)\), establecemos también, al mismo tiempo, la continuidad de \(f\) en \(x\). Debería observarse, no obstante, que el recíproco no es cierto. La continuidad en \(x\) no implica necesariamente la existencia de la derivada \(f'(x)\). Por ejemplo, cuando \(f(x)=|x|\), el punto \(x=0\) es de continuidad de \(f\) (ya que \(f(x)\rightarrow f(0)=0\) cuando \(x\rightarrow0\)), pero no existe derivada en \(0\). El cociente de diferencias \(\frac{f(0+h)-f(0)}{h}\) es igual a \(\frac{|h|}{h}\). Éste vale \(1\) si \(h>0\) y \(-1\) si \(h<0\), y por consiguiente no tiene límite cuando \(h\rightarrow0\).
Referencia bibliográfica. Apostol T. M. (1990. Reimpresión digital 2015): Calculus I. Cálculo con funciones de una variable, con una introducción al álgebra lineal (Reverté Ediciones).
Puedes descargar el artículo completo haciendo clic aquí.
Utilizando distintos métodos de integración se resuelven muchas integrales al nivel de 2º de Bachillerato Científico-Técnico (en la materia de Matemáticas II).
$$\int{\cos^2x\,dx=\begin{bmatrix}u=\cos x&\text{;}&du=-\text{sen}\,x\,dx\\dv=\cos x\,dx&\text{;}&v=\text{sen}\,x\end{bmatrix}}=$$
$$=\text{sen}\,x\cos x+\int{\text{sen}^2x\,dx}=\text{sen}\,x\cos x+x-\int{\cos^2x\,dx}\Rightarrow$$
$$2\int{\cos^2x\,dx}=x+\text{sen}\,x\cos x\Rightarrow\int{\cos^2x\,dx}=\frac{x+\text{sen}\,x\cos x}{2}+C$$
Hay otra forma más rápida de hacer esta integral, pero hemos de recordar una fórmula trigonométrica:
$$\cos 2x=\cos^2x-\text{sen}^2x\Rightarrow\cos 2x=\cos^2x-(1-\cos^2x)\Rightarrow$$
$$\Rightarrow\cos2x=2\cos^2x-1\Rightarrow\cos^2x=\frac{\cos2x+1}{2}$$
Entonces:
$$\int{\cos^2x\,dx}=\int{\frac{\cos2x+1}{2}\,dx}=\int{\frac{1}{2}\,dx}+\int{\frac{\cos2x}{2}\,dx}\Rightarrow$$
$$\Rightarrow\int{\cos^2x\,dx}=\frac{x}{2}+\frac{\text{sen}\,2x}{4}+C=\frac{x+\text{sen}\,x\cos x}{2}+C$$
Utilizando lo anterior:
$$\int{\text{sen}^2x\,dx}=\int{(1-\cos^2x)\,dx}=\int{1\,dx}-\int{\cos^2x\,dx}\Rightarrow$$
$$\int{\text{sen}^2x\,dx}=x-\frac{x+\text{sen}\,x\cos x}{2}+C=\frac{x-\text{sen}\,x\cos x}{2}+C$$
Otra integral fácil de hacer por partes es la siguiente:
$$\int{x\cos x\,dx}=\begin{bmatrix}u=x & \text{;} & du=dx\\dv=\cos x\,dx&\text{;}&v=\text{sen}\,x\end{bmatrix}=$$
$$=x\,\text{sen}\,x-\int{\text{sen}\,x\,dx}\Rightarrow\int{x\cos x\,dx}=x\,\text{sen}\,x+\cos x+C$$
De manera completamente análoga a la anterior:
$$\int{x\,\text{sen}\,x\,dx}=-x\cos x+\text{sen}\,x+C$$
Y, de momento, la última. Esta es inmediata:
$$\int{\text{sen}\,x\cos x\,dx}=\frac{\text{sen}^2x}{2}+C$$
Seguiremos en Integrales indefinidas. Cálculo de primitivas (II).
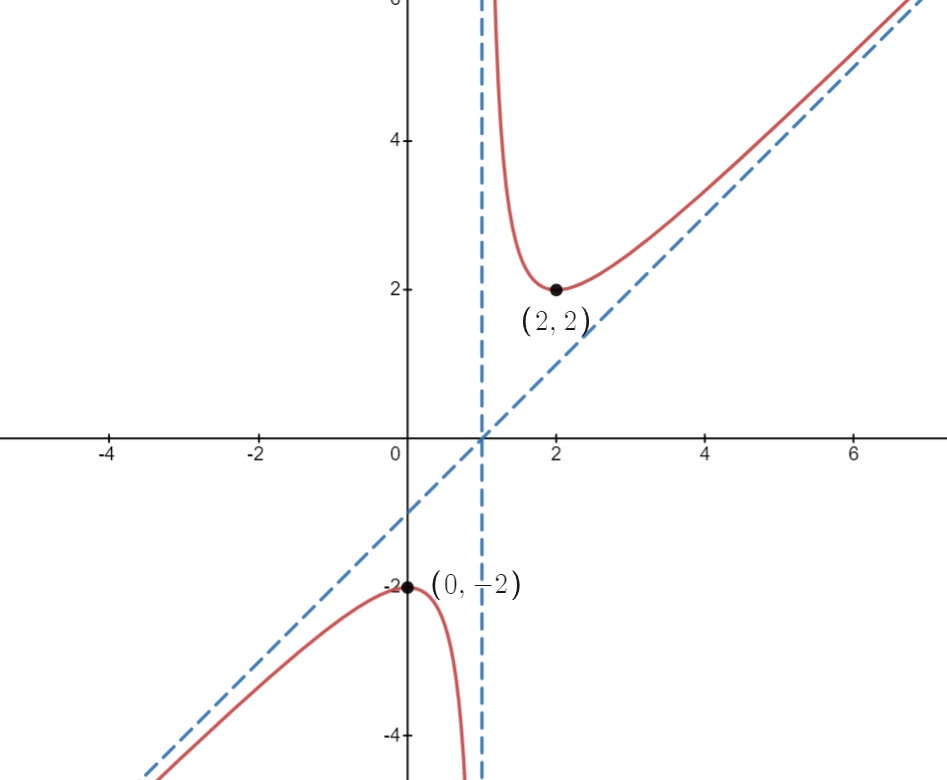
Vamos a hacer un estudio bastante completo de una función racional. Hallaremos su dominio, sus puntos de corte con los ejes y sus asíntotas. También estudiaremos su monotonía (intervalos de crecimiento y decrecimiento), así como sus extremos (máximos y mínimos) relativos.
Recordemos que una función racional es una función como la siguiente:
$$f(x)=\frac{p(x)}{q(x)}$$
donde $p(x)$ y $q(x)$ son polinomios.
Por ejemplo, la función
$$f(x)=\frac{x^2-2x+2}{x-1}$$
se trata de una función racional, y ésta será la función objeto de nuestro estudio.
Dominio
Es fácil darse cuenta de que el denominador de la función se anula para $x=1$. Entonces:
$$\text{Dom}\,f=\mathbb{R}-\{1\}$$
Puntos de corte con los ejes
Los puntos de corte con el eje $X$ son de la forma $(x,0)$. Por tanto, para obtenerlos habremos de resolver la ecuación $f(x)=0\Leftrightarrow\dfrac{x^2-2x+2}{x-1}=0$.
Pero un cociente es cero si el numerador es cero. luego habremos de resolver la ecuación $x^2-2x+2=0$, ecuación de segundo grado que no tiene solución real porque su discriminante es menor que cero: $\Delta=(-2)^2-4\cdot1\cdot2=4-8=-4$.
Por tanto, la gráfica de nuestra función no corta al eje $X$.
Los puntos de corte con el eje $Y$ son de la forma $(0,y)$. Entonces, haciendo $x=0$, obtenemos claramente que $y=-2$. Esto quiere decir que la gráfica de la función corta al eje $Y$ en el punto $(0,-2)$.
Asíntotas
Una recta vertical $x=k$ es una asíntota vertical de una función $f(x)$ si se cumple que
$$\lim_{x\rightarrow k}f(x)=\pm\infty$$
Para que esto pueda ocurrir debemos estudiar el límite en el punto que no pertenece al dominio, es decir, en $x=1$:
$$\mathop {\lim }\limits_{x \to 1} \frac{{{x^2} – 2x + 2}}{{x – 1}} = \left[ {\frac{1}{0}} \right] = \left\{ \begin{array}{lcl} -\infty & \text{ si } & x\to1^- \\ +\infty & \text{ si } & x\to1^+ \\ \end{array} \right.$$
De lo anterior se deduce que $x=1$ es una asíntota vertical.
Una recta vertical $y=k$ es una asíntota horizontal de una función $f(x)$ si se cumple que
$$\lim_{x\to \pm\infty}f(x)=k$$
En nuestro caso:
$$\mathop {\lim }\limits_{x \to \pm\infty} \frac{{{x^2} – 2x + 2}}{{x – 1}} = \left\{ \begin{array}{lcl} +\infty & \text{ si } & x\to+\infty \\ -\infty & \text{ si } & x\to-\infty \\ \end{array} \right.$$
Esto ocurre porque el grado del polinomio del numerador es mayor que el grado del polinomio del denominador. Como el límite en el infinito de la función no es un número real, hemos de deducir que $f$ no tiene asíntotas horizontales.
Una recta de la forma $y=mx+n$ es una asíntota oblicua de una función $f$ si
$$m=\lim_{x\to\pm\infty}\frac{f(x)}{x}\quad;\quad n=\lim_{x\to\pm\infty}\left(f(x)-mx\right)$$
En este caso tenemos:
$$m=\lim_{x\to\pm\infty}\frac{f(x)}{x}=\lim_{x\to\pm\infty}\frac{x^2-2x+2}{x^2-x}=1$$
$$n = \mathop {\lim }\limits_{x \to \infty } \left( {f\left( x \right) – mx} \right) = \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} – 2x + 2}}{{x – 1}} – x} \right) =$$
$$= \mathop {\lim }\limits_{x \to \infty } \left( {\frac{{{x^2} – 2x + 2}}{{x – 1}} – \frac{{{x^2} – x}}{{x – 1}}} \right) = \mathop {\lim }\limits_{x \to \infty } \frac{{ – x + 2}}{{x – 1}} = \frac{{ – 1}}{1} = – 1$$
De lo anterior se deduce que $y=x-1$ es una asíntota oblicua de la función.
Extremos (máximos y mínimos) y monotonía: intervalos de crecimiento y decrecimiento
Si una función $f$ presenta en un punto $x=a$ un máximo o un mínimo relativo, entonces se tiene que $f'(a)=0$. Derivemos pues nuestra función e igualemos a cero.
Usando la regla de derivación de un cociente:
$$f'(x)=\frac{(2x-2)\cdot(x-1)-(x^2-2x+2)\cdot1}{(x-1)^2}=$$
$$=\frac{2x^2-2x-2x+2-x^2+2x-2}{x-1}=\frac{x^2-2x}{(x-1)^2}$$
Entonces
$$f'(x)=0\Leftrightarrow x^2-2x=0\Leftrightarrow x=0\ \text{;}\ x=2$$
Estos dos puntos reciben el nombre de puntos singulares o críticos, a los que vamos a añadir el punto $x=1$ (que no pertenecía al dominio) para elaborar una tabla en la que estudiar el crecimiento y el decrecimiento de la función. Recordemos antes que si $f'(a)>0$, entonces $f$ es creciente en $x=a$, y que si $f'(a)<0$, entonces $f$ es decreciente $x=a$.
$$ \begin{array}{||c|c|c|c|c||} \hline \hline & (-\infty,0) & (0,1) & (1,2) & (2,+\infty)\\\hline f’ & + & – & – & +\\\hline f & \uparrow \uparrow& \downarrow\downarrow & \downarrow\downarrow & \uparrow\uparrow\\\hline \hline\end{array} $$
Por tanto, $f$ es creciente en $(-\infty,0)\cup(2,+\infty)$ y decreciente en $(0,1)\cup(1,2)$. Además, tiene un mínimo relativo en el punto $(0,-2)$ y un máximo relativo en el punto $(2,2)$.
Con todos los datos anteriores no es difícil esbozar la gráfica de la función. Es la siguiente: