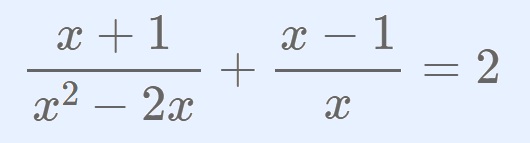Las ecuaciones son más importantes para mí que la política, porque la política es para el momento actual, pero una ecuación es para la eternidad
Si algunos de los términos de una ecuación contienen denominadores en los que aparecen expresiones algebraicas incluyendo la incógnita que se pretende despejar, se pueden suprimir multiplicando todos los términos por el producto de todos ellos o, mejor aún, por su mínimo común múltiplo. Una vez eliminados los denominadores, la ecuación a la que se llega puede ser de las que se saben resolver a un nivel, digamos, de matemáticas de cuarto de Educación Secundaria Obligatoria, es decir, una ecuación de primer o de segundo grado, una bicuadrada o incluso una ecuación con radicales.
Resolvamos, como ejemplo, la ecuación de la imagen superior.
\[\frac{x+1}{x^2-2x}+\frac{x-1}{x}=2\]
Para obtener el mínimo común múltiplo de los denominadores debemos factorizar el primero de ellos: \(x^2-2x=x(x-2)\). Entonces la ecuación es equivalente a esta otra:
\[\frac{x+1}{x(x-2)}+\frac{x-1}{x}=2\]
Ahora es fácil darse cuenta de que el mínimo común múltiplo de los denominadores es, precisamente, \(x^2-2x=x(x-2)\). Multipliquemos por él todos los términos.
$$x(x-2)\cdot\frac{x+1}{x(x-2)}+x(x-2)\cdot\frac{x-1}{x}=x(x-2)\cdot2\Rightarrow$$
$$\Rightarrow x+1+(x-2)(x-1)=2x(x-2)$$
Operando y reduciendo términos semejantes nos queda una ecuación de segundo grado:
$$x+1+x^2-x-2x+2=2x^2-4x\Rightarrow -x^2+2x+3=0\Rightarrow$$
$$\Rightarrow x=\frac{-2\pm\sqrt{2^2-4\cdot(-1)\cdot3}}{2\cdot(-1)}=$$
\[=\frac{-2\pm\sqrt{4+12}}{-2}=\frac{-2\pm\sqrt{16}}{-2}=\frac{-2\pm4}{-2}=\begin{cases}x_1=\dfrac{-2+4}{-2}\Rightarrow x_1=-1\\x_2=\dfrac{-2-4}{-2}\Rightarrow x_2=3 \end{cases}\]
Veamos que ambas soluciones satisfacen la ecuación original.
\[\frac{-1+1}{(-1)^2-2\cdot(-1)}+\frac{-1-1}{-1}=\frac{0}{3}+\frac{-2}{-1}=0+2=2\]
\[\frac{3+1}{3^2-2\cdot3}+\frac{3-1}{3}=\frac{4}{3}+\frac{2}{3}=\frac{6}{3}=2\]
Te propongo, finalmente, que resuelvas las siguientes ecuaciones con la incógnita en el denominador.
a) \(\dfrac{x}{x-1}+\dfrac{2x}{x+1}=3\)
b) \(\dfrac{5}{x+2}+\dfrac{x}{x+3}=\dfrac{3}{2}\)
c) \(\dfrac{1}{x}+\dfrac{1}{x^2}=\dfrac{3}{4}\)
d) \(\dfrac{x+1}{x+5}+\dfrac{1-x}{x-4}=\dfrac{5}{2}\)
e) \(\dfrac{x+7}{x+3}+\dfrac{x^2-3x+6}{x^2+2x-3}=1\)