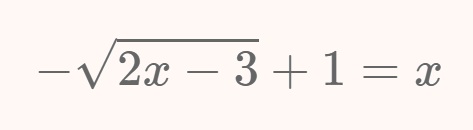Podrán cortar todas las flores, pero no podrán detener la primavera
En este tipo de ecuaciones la incógnita se encuentra bajo el signo radical. Nos vamos a ceñir al caso en que la incógnita se encuentra bajo una raíz cuadrada. Para resolver este tipo de ecuaciones se aísla la raíz (o una de las raíces si hay más de una) en uno de los miembros y luego se elevan los dos miembros al cuadrado. Si la ecuación original tiene más de una raíz habrá que volver a repetir este proceso.
En este procedimiento, al elevar al cuadrado ambos miembros de la igualdad, pueden aparecer soluciones que no lo son de la ecuación original y que, por tanto, habría que rechazar. Por ello, en este tipo de ecuaciones es de obligado cumplimiento comprobar todas las soluciones en la ecuación original y rechazar aquéllas que no se adecúen a la misma.
Lo veremos mejor con un par de ejemplos.
Ejemplo 1
En este primer ejemplo resolveremos la ecuación de la imagen superior:
\[-\sqrt{2x-3}+1=x\]
Aislamos el radical restando uno en los dos miembros. Luego elevamos al cuadrado y resolvemos la ecuación resultante:
\[-\sqrt{2x-3}=x-1\Rightarrow \left(-\sqrt{2x-3}\right)^2=(x-1)^2\Rightarrow 2x-3=x^2-2x+1\Rightarrow\]
\[\Rightarrow x^2-4x+4=0\Rightarrow x=\frac{4\pm\sqrt{(-4)^2-4\cdot1\cdot4}}{2\cdot1}=\frac{4\pm\sqrt{16-16}}{2}=\frac{4}{2}=2\]
La ecuación de segundo grado anterior se podría haber resuelto sin echar mano de la fórmula pues:
\[x^2-4x+4=0\Rightarrow(x-2)^2=0\Rightarrow x-2=0\Rightarrow x=2\]
Ahora comprobamos si esta solución se cumple en la ecuación original.
\[-\sqrt{2\cdot2-3}+1=-\sqrt{4-3}+1=-\sqrt{1}+1=-1+1=0\neq2\]
Por tanto \(x=2\) no es solución de la ecuación \(-\sqrt{2x-3}+1=x\). Observa que si la ecuación original hubiera sido \(\sqrt{2x-3}+1=x\), entonces sí que \(x=2\) sería una solución de esta última.
Ejemplo 2
Resolver la siguiente ecuación:
\[\sqrt{2x-1}+\sqrt{x+4}=6\]
Esta ecuación tiene dos radicales. Para resolverla aislamos uno de ellos y elevamos al cuadrado. Luego tendremos que volver a repetir el proceso.
\[\sqrt{2x-1}+\sqrt{x+4}=6\Rightarrow\sqrt{2x-1}=6-\sqrt{x+4}\Rightarrow (\sqrt{2x-1})^2=(6-\sqrt{x+4})^2\Rightarrow\]
\[\Rightarrow2x-1=36-12\sqrt{x+4}+x+4\Rightarrow12\sqrt{x+4}=41-x\]
Observa que, tras aislar el primer radical y elevar ambos miembros al cuadrado, la ecuación todavía tiene un radical en el que se encuentra la incógnita. Pues bien, este lo hemos pasado al primer miembro y el resto de términos al segundo, reduciendo los que son semejantes. Ahora volvemos a elevar al cuadrado.
\[(12\sqrt{x+4})^2=(41-x)^2\Rightarrow 144(x+4)=1681-82x+x^2\Rightarrow\]
\[\Rightarrow144x+576=1681-82x+x^2\Rightarrow x^2-226x+1105=0\Rightarrow\]
\[x=\frac{226\pm\sqrt{(-226)^2-4\cdot1\cdot1105}}{2\cdot1}=\frac{51076\pm\sqrt{4420}}{2}=\frac{226\pm\sqrt{46656}}{2}=\]
\[=\frac{226\pm216}{2}=\begin{cases}x_1=\frac{442}{2}\Rightarrow x_1=221\\x_2=\frac{10}{2}\Rightarrow x_2=5\end{cases}\]
Comprobemos ahora si estos valores verifican o no la ecuación original:
\[\sqrt{2\cdot221-1}+\sqrt{221+4}=\sqrt{441}+\sqrt{225}=21+15=36\neq6\]
\[\sqrt{2\cdot5-1}+\sqrt{5+4}=\sqrt{9}+\sqrt{9}=3+3=6\]
Por tanto la única solución de la ecuación original, \(\sqrt{2x-1}+\sqrt{x+4}=6\), es \(x=5\).
Te propongo, finalmente, que intentes resolver las siguientes ecuaciones con radicales o ecuaciones irracionales:
a) \(\sqrt{5x+6}=3+2x\)
b) \(x+\sqrt{7-3x}=1\)
c) \(\sqrt{2-5x}+x\sqrt{3}=0\)
d) \(\sqrt{2x}+\sqrt{5x-6}=4\)
e) \(\sqrt{3x+3}-1=\sqrt{8-2x}\)
f) \(\sqrt{\dfrac{7x+1}{4}}=\dfrac{5x-7}{6}\)