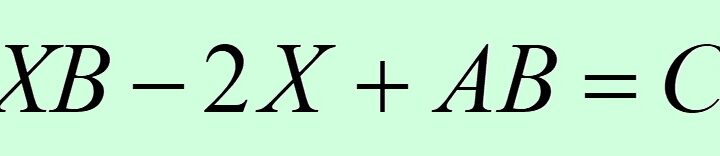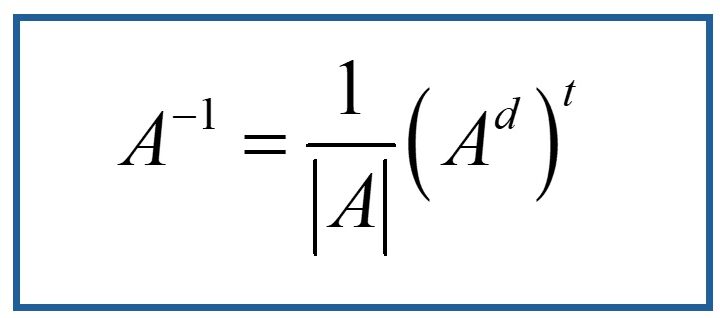Podrán cortar todas las flores, pero no podrán detener la primavera

Pablo Neruda

---

En este tipo de ecuaciones la incógnita se encuentra bajo el signo radical. Nos vamos a ceñir al caso en que la incógnita se encuentra bajo una raíz cuadrada. Para resolver este tipo de ecuaciones se aísla la raíz (o una de las raíces si hay más de una) en uno de los miembros y luego se elevan los dos miembros al cuadrado. Si la ecuación original tiene más de una raíz habrá que volver a repetir este proceso.

En este procedimiento, al elevar al cuadrado ambos miembros de la igualdad, pueden aparecer soluciones que no lo son de la ecuación original y que, por tanto, habría que rechazar. Por ello, en este tipo de ecuaciones es de obligado cumplimiento comprobar todas las soluciones en la ecuación original y rechazar aquéllas que no se adecúen a la misma.

Lo veremos mejor con un par de ejemplos.

Ejemplo 1

En este primer ejemplo resolveremos la ecuación de la imagen superior: 

$$-\sqrt{2x-3}+1=x$$

Aislamos el radical restando uno en los dos miembros. Luego elevamos al cuadrado y resolvemos la ecuación resultante:

$$-\sqrt{2x-3}=x-1\Rightarrow {(-\sqrt{2x-3})}^2=(x-1{)}^2\Rightarrow 2x-3=x^2-2x+1\Rightarrow$$

$$\Rightarrow x^2-4x+4=0\Rightarrow x=\frac{4\pm \sqrt{(-4{)}^2-4\cdot 1\cdot 4}}{2\cdot 1}=\frac{4\pm \sqrt{16-16}}{2}=\frac{4}{2}=2$$

La ecuación de segundo grado anterior se podría haber resuelto sin echar mano de la fórmula pues:

$$x^2-4x+4=0\Rightarrow (x-2{)}^2=0\Rightarrow x-2=0\Rightarrow x=2$$

Ahora comprobamos si esta solución se cumple en la ecuación original.

$$-\sqrt{2\cdot 2-3}+1=-\sqrt{4-3}+1=-\sqrt{1}+1=-1+1=0\ne 2$$

Por tanto $x=2$ no es solución de la ecuación $-\sqrt{2x-3}+1=x$. Observa que si la ecuación original hubiera sido $\sqrt{2x-3}+1=x$, entonces sí que $x=2$ sería una solución de esta última.

Ejemplo 2

Resolver la siguiente ecuación:

$$\sqrt{2x-1}+\sqrt{x+4}=6$$

Esta ecuación tiene dos radicales. Para resolverla aislamos uno de ellos y elevamos al cuadrado. Luego tendremos que volver a repetir el proceso.

$$\sqrt{2x-1}+\sqrt{x+4}=6\Rightarrow \sqrt{2x-1}=6-\sqrt{x+4}\Rightarrow (\sqrt{2x-1}{)}^2=(6-\sqrt{x+4}{)}^2\Rightarrow$$

$$\Rightarrow 2x-1=36-12\sqrt{x+4}+x+4\Rightarrow 12\sqrt{x+4}=41-x$$

Observa que, tras aislar el primer radical y elevar ambos miembros al cuadrado, la ecuación todavía tiene un radical en el que se encuentra la incógnita. Pues bien, este lo hemos pasado al primer miembro y el resto de términos al segundo, reduciendo los que son semejantes. Ahora volvemos a elevar al cuadrado.

$$(12\sqrt{x+4}{)}^2=(41-x{)}^2\Rightarrow 144(x+4)=1681-82x+x^2\Rightarrow$$

$$\Rightarrow 144x+576=1681-82x+x^2\Rightarrow x^2-226x+1105=0\Rightarrow$$

$$x=\frac{226\pm \sqrt{(-226{)}^2-4\cdot 1\cdot 1105}}{2\cdot 1}=\frac{51076\pm \sqrt{4420}}{2}=\frac{226\pm \sqrt{46656}}{2}=$$

$$=\frac{226\pm 216}{2}=\{\begin{array}{l}{x}_1=\frac{442}{2}\Rightarrow x_1=221\\ x_2=\frac{10}{2}\Rightarrow x_2=5\end{array}$$

Comprobemos ahora si estos valores verifican o no la ecuación original:

$$\sqrt{2\cdot 221-1}+\sqrt{221+4}=\sqrt{441}+\sqrt{225}=21+15=36\ne 6$$

$$\sqrt{2\cdot 5-1}+\sqrt{5+4}=\sqrt{9}+\sqrt{9}=3+3=6$$

Por tanto la única solución de la ecuación original, $\sqrt{2x-1}+\sqrt{x+4}=6$, es $x=5$.

Te propongo, finalmente, que intentes resolver las siguientes ecuaciones con radicales o ecuaciones irracionales:

a) $\sqrt{5x+6}=3+2x$

b) $x+\sqrt{7-3x}=1$

c) $\sqrt{2-5x}+x\sqrt{3}=0$

d) $\sqrt{2x}+\sqrt{5x-6}=4$

e) $\sqrt{3x+3}-1=\sqrt{8-2x}$

f) $\sqrt{{\displaystyle \frac{7x+1}{4}}}={\displaystyle \frac{5x-7}{6}}$

¿Para qué repetir los errores antiguos habiendo tantos errores nuevos que cometer?

Bertrand Russell

---

Una ecuación bicuadrada es una ecuación de cuarto grado a la que le faltan los términos de grado impar.

$$a{x}^4+b{x}^2+c=0a\ne 0$$

Para resolverlas se realiza el cambio de variable $x^2=z$, y entonces ocurre lo siguiente:

$$a{x}^4+b{x}^2+c=0\Rightarrow a{\left(x^2\right)}^2+b{x}^2+c=0\Rightarrow a{z}^2+bz+c=0$$

Esta última es una ecuación de segundo grado cuya incógnita es ahora $z$. Ahora, para obtener las soluciones de la ecuación original hay que deshacer el cambio.

Es decir, si $z$ es una solución positiva de la última ecuación de segundo grado, tendremos dos soluciones $x_1$ y $x_2$ para la bicuadrada:

$$x^2=z\Rightarrow \{\begin{array}{l}{x}_1=+\sqrt{z}\\ x_2=-\sqrt{z}\end{array}$$

En el caso de que $z=0$ sea una solución de la de segundo grado, también $x=0$ será una solución de la bicuadrada, pues de $x^2=0$ se deduce $x=0$.

Finalmente, una solución negativa $z$ de $a{z}^2+bz+c=0$ no lleva asociada ninguna solución real de la bicuadrada ya que la ecuación $x^2=z$ carece de soluciones reales al ser $z<0$.

Mejor veamos todo lo anterior con un ejemplo concreto.

Para resolver la ecuación de la imagen que encabeza este artículo, $x^4-10x^2+9=0$, realizamos el cambio de variable mencionado, $x^2=z$, con lo que la ecuación bicuadrada se convierte en la ecuación de segundo grado $z^2-10z+9=0$. Resolviendo esta última se tiene:

$$z=\frac{10\pm \sqrt{(-10{)}^2-4\cdot 1\cdot 9}}{2\cdot 1}=\frac{10\pm \sqrt{100-36}}{2}=\frac{10\pm \sqrt{64}}{2}=$$

$$=\frac{10\pm 8}{2}=\{\begin{array}{l}{z}_1={\displaystyle \frac{10+8}{2}\Rightarrow z_1=9}\\ z_2={\displaystyle \frac{10-8}{2}\Rightarrow z_2=1}\end{array}$$

Ahora deshacemos el cambio para obtener las soluciones de la ecuación bicuadrada.

Para $z_1=9$ es $x^2=9\Rightarrow x=\sqrt{9}\Rightarrow {\displaystyle \{\begin{array}{l}{x}_1=3\\ x_2=-3\end{array}}$.

Para $z_2=1$ es $x^2=1\Rightarrow x=\sqrt{1}\Rightarrow {\displaystyle \{\begin{array}{l}{x}_3=1\\ x_4=-1\end{array}}$.

Te propongo, finalmente, que resuelvas las siguientes ecuaciones:

a) $x^4-9x^2+20=0$

b) $4x^4-5x^2+1=0$

c) $x^4-18x^2+81=0$

d) ${(x^2+1)}^2+6=5(x^2+1)$

e) ${(2x^2+1)}^2-5=(x^2+2)(x^2-2)$

El modo de dar una vez en el clavo es dar cien veces en la herradura

Miguel de Unamuno

---

Dado un polinomio de grado $n$,

$$p(x)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_2{x}^2+a_1{x}^1+a_0,a_n\ne 0$$

nos planteamos como objetivo resolver la ecuación

$$p(x)=0$$

Si $n=1$ la ecuación anterior es de primer grado y la podemos escribir de la forma

$$ax+b=0$$

con $a\ne 0$, cuya solución es

$${\displaystyle x=-\frac{b}{a}}$$

Si $n=2$ la ecuación toma la forma de la conocida ecuación de segundo grado:

$$a{x}^2+bx+c=0,a\ne 0$$

Esta sección no es de necesaria lectura para alumnos de 4º de ESO.

Una manera de obtener la solución se expone a continuación.

Multiplicando por $4a$ los dos miembros de la igualdad obtenemos:

$$4a^2{x}^2+4abx+4ac=0$$

Sumando y restando $b^2$ en el primer miembro podemos escribir:

$$(4a^2{x}^2+4abx+b^2)-b^2+4ac=0$$

Obsérvese que lo que hay en el interior del paréntesis es el cuadrado de la suma $2ax+b$. Por tanto, la ecuación anterior la podemos escribir ahora así:

$${(2ax+b)}^2=b^2-4ac$$

Teniendo en cuenta que las soluciones de la ecuación $x^2=a$ son $x=\pm \sqrt{a}$, se deduce ahora fácilmente que:

$$2ax+b=\pm \sqrt{b^2-4ac}$$

Despejando $x$:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

---

Para hallar las soluciones se aplica la siguiente fórmula:

$$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$$

En la fórmula anterior, la expresión $b^2-4ac$ recibe el nombre de discriminante de la ecuación de segundo grado y se le suele denotar con la letra griega delta mayúscula: $\mathrm{\Delta }=b^2-4ac$. Si $\mathrm{\Delta }>0$ la ecuación de segundo grado tienen dos soluciones reales, si $\mathrm{\Delta }=0$ tiene sólo una (doble) y , finalmente, si $\mathrm{\Delta }<0$ la ecuación no tiene raíces reales.

Como ejemplo, resolvamos la siguiente ecuación:

$${\displaystyle \frac{2x^2+x}{2}-\frac{6x+3}{8}=\frac{x}{2}}$$

En primer lugar, para eliminar los denominadores, multiplicamos todos los términos por el mínimo común múltiplo de los denominadores, que es $8$:

$$8\cdot \frac{2x^2+x}{2}-8\cdot \frac{6x+3}{8}=8\cdot \frac{x}{2}\Rightarrow$$

$$\Rightarrow 4(2x^2+x)-1(6x+3)=4x\Rightarrow 8x^2+4x-6x-3=4x$$

Ahora pasamos todos los términos al primer miembro para obtener una ecuación de segundo grado en su forma general:

$$8x^2+4x-6x-3-4x=0\Rightarrow 8x^2-6x-3=0$$

Y, finalmente aplicamos la fórmula para obtener las soluciones de la ecuación de segundo grado. Tendremos en cuenta que los coeficientes son $a=8$, $b=-6$, $c=-3$.

$$x=\frac{-(-6)\pm \sqrt{(-6{)}^2-4\cdot 8\cdot (-3)}}{2\cdot 8}=\frac{6\pm \sqrt{36-(-96)}}{16}=\frac{6\pm \sqrt{132}}{16}=$$

$$=\frac{6\pm 2\sqrt{33}}{16}=\{\begin{array}{l}{\displaystyle x_1=\frac{6+2\sqrt{33}}{16}=\frac{3+\sqrt{33}}{8}\cong 1,093}\\ {\displaystyle x_2=\frac{6-2\sqrt{33}}{16}=\frac{3-\sqrt{33}}{8}\cong -0,343}\end{array}$$

Esta sección no es de necesaria lectura para alumnos de 4º de ESO.

Si el grado del polinomio $p(x)$ es tres o cuatro nos encontramos con ecuaciones cúbicas y cuárticas. Las fórmulas y resolución de este tipo de ecuaciones escapa a los objetivos de las matemáticas de secundaria y bachillerato. En cualquier caso, para alumnos que cursen estudios universitarios, recomiendo el sititio Web de Carlos Iborra y sus apuntes sobre las fórmulas de Cardano-Ferrari. Transcribo aquí un parrafo que aparece al principio de tales apuntes.

También es conocido que Tartaglia y Cardano encontraron una fórmula análoga para ecuaciones cúbicas (en la que aparecen raíces cúbicas además de cuadradadas) y que Ferrari encontró otra más compleja para ecuaciones cuárticas. En realidad, más que fórmulas, encontraron métodos de resolución que pueden resumirse en sendas fórmulas, si bien en el caso de las ecuaciones cuárticas, la fórmula es tan compleja que resulta inmanejable, y es preferible describir el proceso de resolución como un algoritmo de varios pasos. Por último, Abel demostró que, para $n>4$, no existen fórmulas análogas que expresen las raíces de la ecuación general de grado $n$ en función de sus coeficientes a través de sumas, productos, cocientes y extracción de raíces, lo que convierte a las fórmulas de Cardano-Ferrari en dos singularidades algebraicas.

---

En la materia de matemáticas de 4º de ESO (Educación Secundaria Obligatoria) se resuelven algunas ecuaciones polinómicas de grado superior a tres, siempre y cuando algunas de sus raíces sean enteras (recuérdese que decir raíz de un polinomio es lo mismo que decir solución de la correspondiente ecuación polinómica, es más, a veces se utiliza el término raíz en vez del término solución de una ecuación).

Para resolver estas ecuaciones polinómicas de grado superior a tres se utiliza la conocida regla de Ruffini y el teorema del resto, según el cual, el resto $r$ de dividir un polinomio $p(x)$ entre el binomio $x-a$ coincide con el valor numérico para $x=a$, es decir, $r=p(a)$. En particular, si $x=a$ es una raíz de $p(x)$, tenemos que $p(a)=0$ y consecuentemente el resto de dividir $p(x)$ entre $x-a$ será igual a $0$. Así pues el polinomio $p(x)$ factoriza de la forma $p(x)=(x-a)c(x)$, donde $c(x)$ es el cociente de la división. Podemos buscar ahora las raíces de $c(x)$ y continuar con el proceso. Hay un importante resultado según el cual las posibles raíces enteras de un polinomio $p(x)$ se encuentran entre los divisores del término independiente. De este modo es fácil encontrar las raíces enteras de un polinomio (incluso algunas más que no sean enteras), y por tanto las soluciones (o raíces) de la correspondiente ecuación polinómica. Además tendremos una descomposición del polinomio en factores. Veámoslo en el siguiente ejemplo.

Resolver la siguiente ecuación:

$$x^7+2x^6-5x^5-19x^4-26x^3-19x^2-6x=0$$

Las soluciones de la ecuación son las raíces del polinomio

$$x^7+2x^6-5x^5-19x^4-26x^3-19x^2-6x$$

Una raíz es claramente $x=0$ (el término independiente del polinomio es cero). Extrayendo factor común tenemos:

$$x(x^6+2x^5-5x^4-19x^3-26x^2-19x-6)$$

Ahora factorizamos el polinomio $x^6+2x^5-5x^4-19x^3-26x^2-19x-6$. Para ello utilizamos la regla de Ruffini probando con los divisores del término independiente: $\text{Div}(-6)=\{\pm 1\pm 2\pm 3\pm 6\}$.

$$\begin{array}{rrrrrrrr}& 1& 2& -5& -19& -26& -19& -6\\ -1& & -1& -1& 6& 13& 13& 6\\ & 1& 1& -6& -13& -13& -6& 0\\ -1& & -1& 0& 6& 7& 6& \\ & 1& 0& -6& -7& -6& 0& \\ -2& & -2& 4& 4& 6& & \\ & 1& -2& -2& -3& 0& & \\ 3& & 3& 3& 3& & & \\ & 1& 1& 1& 0& & & \end{array}$$

Si seguimos probando con el resto de divisores del término independiente no volvemos a obtener resto cero. Esto quiere decir que las raíces enteras del polinomio son $-1$ (doble), $-2$ y $3$, y que la factorización del polinomio queda de la forma:

$$x^7+2x^6-5x^5-19x^4-26x^3-19x^2-6x=x(x+1{)}^2(x+2)(x-3)(x^2+x+1)$$

El resto de raíces habría que encontrarlas resolviendo la ecuación de segundo grado $x^2+x+1=0$, ecuación que no tiene soluciones reales pues su discriminante es menor que cero:

$$\mathrm{\Delta }=1^2-4\cdot 1\cdot 1=1-4=-3<0$$

De todo lo anterior se desprende que las soluciones de la ecuación 

$$x^7+2x^6-5x^5-19x^4-26x^3-19x^2-6x=0$$

son:

$$x_1=0,x_2=-1\text{(doble)},x_3=-2,x_4=3$$

Según lo comentado anteriormente, cada vez que encontremos una raíz entera $a$, tendremos que $x-a$ es un factor del polinomio $p(x)$. Si $a$ vuelve a ser raíz del cociente obtenido se dice que es una raíz doble y $x-a$ volverá a ser un factor del polinomio original $p(x)$. De este modo una raíz puede ser simple, doble, triple, etcétera.

Esta sección no es de necesaria lectura para alumnos de 4º de ESO.

Según el teorema fundamental del álgebra, todo polinomio de grado $n$ tiene $n$ raíces. Pero no todas ellas tienen que ser reales, algunas pueden ser raíces complejas. Además, estás últimas, siempre aparecen en parejas de números complejos conjugados. Como la teoría de números complejos no se estudia en las matemáticas de la Educación Secundaria Obligatoria (si acaso se ven «de pasada» en la materia Matemáticas I, de 1º de Bachillerato Científico-Tecnológico), podremos factorizar un polinomio obteniendo factores de grado uno de la forma $x-a$ y de grado dos de la forma $x^2+bx+c$ que no tengan raíces reales, llamados polinomos irreducibles. A no ser que el polinomio tenga varias parejas de raíces complejas conjugadas y entonces, a un nivel de matemáticas de Secundaria o Bachillerato, habremos de incluir factores irreducibles de grado par mayor que dos. No será este el caso que nos ocupe, desde luego, en el caso particular de las matemáticas de 4º de ESO.

En cualquier caso finalizaremos la factorización del ejemplo anterior resolviendo la ecuación $x^2+x+1=0$ y llamando $i=\sqrt{-1}$, que es la unidad imaginaria, el número complejo más conocido y desde el que parte toda la teoría de números complejos. Entre otras cosas porque cualquier estudiante de secundaria que conozca la ecuación de segundo grado es capaz de entender perfectamente este proceso y, al menos, nos habremos acercado un poco a los números complejos.

Resolvamos, finalmente, la ecuación

$$x^2+x+1=0$$

En este caso los coeficientes son $a=b=c=1$. Por tanto:

$$x=\frac{-1\pm \sqrt{1^2-4\cdot 1\cdot 1}}{2\cdot 1}=\frac{-1\pm \sqrt{1-4}}{2}=\frac{-1\pm \sqrt{-3}}{2}=$$

$$=\frac{-1\pm \sqrt{3}\sqrt{-1}}{2}=\frac{-1\pm \sqrt{3}i}{2}=\{\begin{array}{l}{\displaystyle x_1=\frac{-1+\sqrt{3}i}{2}=-\frac{1}{2}+\frac{\sqrt{3}}{2}i}\\ {\displaystyle x_2=\frac{-1-\sqrt{3}i}{2}=-\frac{1}{2}-\frac{\sqrt{3}}{2}i}\end{array}$$

Las soluciones anteriores (obsérvese que son conjugadas, una es de la forma $x_1=p+q$ y otra de la forma $x_2=p-q$) son también las raíces del polinomio $x^2+x+1$. Esto quiere decir que el polinomio factoriza de la forma $(x-x_1)(x-x_2)$, es decir:

$$x^2+x+1=(x-(-\frac{1}{2}+\frac{\sqrt{3}}{2}i))(x-(-\frac{1}{2}-\frac{\sqrt{3}}{2}i))=$$

$$=(x+\frac{1}{2}-\frac{\sqrt{3}}{2}i)(x+\frac{1}{2}+\frac{\sqrt{3}}{2}i)$$

---

Adoramos el caos porque amamos producir orden

M. C. Escher

---

Un ecuación matricial es una ecuación donde la incógnita es una matriz. La ecuación matricial más sencilla es de la forma $AX=B$, donde $A$ es una matriz cuadrada, $B$ es otra matriz y $X$ es la matriz incógnita. La ecuación de primer grado más sencilla también es $ax=b$, donde $a$ y $b$ son números reales y $x$ es la incógnita. Si $a\ne 0$, la solución es $x=\frac{b}{a}$. Si $a=0$, tenemos que $0x=0$, con lo que $b=0$ y cualquier número $x$ es solución. Por eso, si $a=0$, la ecuación no tiene interés alguno. Centrémonos pues en el caso $a\ne 0$. ¿Por qué $x=\frac{b}{a}$ es solución de la ecuación? No es difícil de demostrar. Sabemos que si $a\ne 0$, el número $a$ tiene inverso, $a^{-1}=\frac{1}{a}$. El inverso de un número $a\ne 0$, tiene la característica de que al multiplicarlo por $a$ se obtiene el número $1$ (el uno es el elemento neutro de la multiplicación de números reales). De este modo:

$$ax=b\iff a^{–1}ax=a^{–1}b\iff 1x=\frac{1}{a}b\iff x=\frac{b}{a}$$

Así, por ejemplo, la solución de la ecuación $-3x=4$ es $x=\frac{4}{-3}=-\frac{4}{3}$. Nos han enseñado que “lo que está multiplicando pasa al otro miembro dividiendo”. Esta regla tan extendida debería de usarse menos. En realidad, lo que se hace es dividir los dos miembros de la igualdad entre $-3$ o, mejor, multiplicar los dos miembros de la igualdad por el inverso de $-3$, que es ${\left(–3\right)}^{–1}=\frac{1}{–3}=–\frac{1}{3}$. Esta es la propiedad que realmente deberíamos de retener: “si multiplicamos o dividimos los dos miembros de una igualdad por un mismo número (distinto de cero en el caso de que dividamos), la igualdad se mantiene o no varía”.

Como no sabemos dividir matrices, sí que podemos proceder como anteriormente, multiplicando a la izquierda de ambos miembros por $A^{-1}$, para resolver la ecuación $AX=B$:

$$AX=B\iff A^{–1}AX=A^{–1}B\iff IX=A^{–1}B\iff X=A^{–1}B$$

Recuerda que $I$ es la matriz identidad. En el caso de orden 3 es $I=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$. Además, $A{A}^{–1}=A^{–1}A=I$.

La ecuación matricial $AX=B$ es muy útil para resolver sistemas de ecuaciones, en particular sistemas de tres ecuaciones con tres incógnitas. Veamos un ejemplo.

Consideremos el siguiente sistema de ecuaciones:

$$\{\begin{array}{l}2x+y=0\\ y+3z=10\\ 2x+y+z=8\end{array}$$

Este sistema lo podemos reescribir matricialmente así:

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\left(\begin{array}{c}4\\ 10\\ 8\end{array}\right)$$

Si llamamos $A=\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)$, $X=\left(\begin{array}{c}x\\ y\\ z\end{array}\right)$ y $B=\left(\begin{array}{c}4\\ 10\\ 8\end{array}\right)$, el sistema adopta la forma de una ecuación matricial del tipo $AX=B$, cuya solución sabemos que es $X=A{B}^{-1}$.

La inversa de la matriz $A=\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)$ es $A^{-1}=\left(\begin{array}{ccc}-1& -\frac{1}{2}& \frac{3}{2}\\ 3& 1& -3\\ -1& 0& 1\end{array}\right)$. Entonces:

$$X=A^{-1}B=\left(\begin{array}{ccc}-1& -\frac{1}{2}& \frac{3}{2}\\ 3& 1& -3\\ -1& 0& 1\end{array}\right)\left(\begin{array}{c}4\\ 10\\ 8\end{array}\right)\Rightarrow X=\left(\begin{array}{c}3\\ -2\\ 4\end{array}\right)$$

Por tanto, las soluciones del sistema son $x=3$., $y=-2$, $z=4$.

Los matemáticos dedicaron muchos esfuerzos a la resolución de ecuaciones y de sistemas de ecuaciones. De hecho, las soluciones del sistema anterior se pueden obtener aplicando una curiosa regla, llamada regla de Cramer. Pensemos en un sistema cualquiera de tres ecuaciones con tres incógnitas que tenga solución única (hay sistemas que no tienen solución y sistemas que tienen infinitas soluciones):

$$\{\begin{array}{l}{a}_{11}x+a_{12}y+a_{13}z=b_1\\ a_{21}x+a_{22}y+a_{23}z=b_2\\ a_{31}x+a_{32}y+a_{33}z=b_3\end{array}$$

La matriz $A$ se llama matriz de los coeficientes. Esta matriz debe de ser regular o invertible, es decir, debe de tener determinante distinto de cero: $\left|A\right|\ne 0$. La matriz $B$ es la matriz de los términos independientes y la matriz $X$ es la matriz incógnita.

Pues bien, la regla de Cramer dice que las incógnitas pueden calcularse del siguiente modo:

$$x=\frac{\left|\begin{array}{ccc}{b}_1& a_{12}& a_{13}\\ b_2& a_{22}& a_{23}\\ b_3& a_{32}& a_{33}\end{array}\right|}{\left|A\right|}\text{;}y=\frac{\left|\begin{array}{ccc}{a}_{11}& b_1& a_{13}\\ a_{21}& b_2& a_{23}\\ a_{31}& b_3& a_{33}\end{array}\right|}{\left|A\right|}\text{;}z=\frac{\left|\begin{array}{ccc}{a}_{11}& a_{12}& b_1\\ a_{21}& a_{22}& b_2\\ a_{31}& a_{32}& b_3\end{array}\right|}{\left|A\right|}$$

En nuestro ejemplo, $\left|A\right|=2$. Por tanto:

$$x=\frac{\left|\begin{array}{ccc}4& 1& 0\\ 10& 1& 3\\ 8& 1& 1\end{array}\right|}{2}=\frac{(4+24+0)-(0+10+12)}{2}=\frac{28-22}{2}=\frac{6}{2}\Rightarrow x=3$$

$$y=\frac{\left|\begin{array}{ccc}2& 4& 0\\ 0& 10& 3\\ 2& 8& 1\end{array}\right|}{2}=\frac{(20+24+0)-(0+0+48)}{2}=\frac{44-48}{2}=\frac{-4}{2}\Rightarrow y=-2$$

$$z=\frac{\left|\begin{array}{ccc}2& 1& 4\\ 0& 1& 10\\ 2& 1& 8\end{array}\right|}{2}=\frac{(16+20+0)-(8+0+20)}{2}=\frac{36-28}{2}=\frac{8}{2}\Rightarrow z=4$$

¿Por qué funciona esta regla? Bueno, no lo vamos a hacer aquí, pero un buen ejercicio sería intentar demostrarla.

En general, la inversa de una matriz sirve para calcular ecuaciones matriciales de muchos tipos. Hagamos otro ejemplo.

El siguiente problema se propuso en el año 2019 en Castilla-La Mancha.

Enunciado

Dadas las matrices $A=\left(\begin{array}{ccc}-1& -1& -1\\ -1& 1& 0\\ 2& -1& 0\end{array}\right)$, $B=\left(\begin{array}{ccc}1& 2& 2\\ 0& 1& 1\\ 1& -1& 2\end{array}\right)$ y $C=\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\\ 0& 1& 2\end{array}\right)$, calcular razonadamente la matriz $X$ que verifica $AX-2B=C$.

Solución

En primer lugar, calcularemos la inversa de la matriz $A$.

$\left|A\right|=(0+0+1)-(-2+0+0)=-1+2=1$. Como $\left|A\right|\ne 0$, existe la inversa de $A$.

La matriz adjunta de $A$ es $A^d=\left(\begin{array}{ccc}0& 0& -1\\ 1& 2& 3\\ 1& 1& -2\end{array}\right)$. Entonces:

$$A^{-1}=\frac{1}{\left|A\right|}{\left(A^d\right)}^t=\frac{1}{1}\left(\begin{array}{ccc}0& 1& 1\\ 0& 2& 1\\ -1& -3& -2\end{array}\right)\Rightarrow A^{-1}=\left(\begin{array}{ccc}0& 1& 1\\ 0& 2& 1\\ -1& -3& -2\end{array}\right)$$

Resolvamos ahora la ecuación matricial. Lo primero es despejar la matriz incógnita $X$:

$$AX–2B=C\Rightarrow AX=C+2B\Rightarrow A^{–1}AX=A^{–1}\left(C+2B\right)\Rightarrow X=A^{–1}\left(C+2B\right)$$

Obsérvese que hemos multiplicado por la inversa de $A$ por la izquierda en ambos miembros de la igualdad. No se puede hacer por la derecha porque las matrices no cumplen la propiedad conmutativa y, en principio, $AX{A}^{–1}\ne A^{–1}AX$. Ahora, operando:

$$X=\left(\begin{array}{ccc}0& 1& 1\\ 0& 2& 1\\ -1& -3& -2\end{array}\right)\cdot [\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\\ 0& 1& 2\end{array}\right)+2\left(\begin{array}{ccc}1& 2& 2\\ 0& 1& 1\\ 1& -1& 2\end{array}\right)]=$$

$$=\left(\begin{array}{ccc}0& 1& 1\\ 0& 2& 1\\ -1& -3& -2\end{array}\right)\cdot \left(\begin{array}{ccc}2& 5& 5\\ 1& 3& 2\\ 2& -1& -6\end{array}\right)=\left(\begin{array}{ccc}3& 2& 8\\ 4& 5& 10\\ -9& -12& -23\end{array}\right)$$

Supongamos ahora que, con las mismas matrices que en el ejercicio anterior, la ecuación matricial que se pide resolver es la siguiente:

$$XB-2X+AB=C$$

Esta ecuación matricial es un poco más complicada que la anterior. En primer lugar, vamos a pasar al segundo miembro los términos que no contienen la incógnita:

$$XB-2X=C-AB$$

Ahora, para despejar la incógnita $X$, debemos de sacarla factor común en el primer miembro. Pero no debemos de extraerla así: $X(B-2)$. Esto es porque no tiene sentido realizar la resta $B-2$, es decir, no se  puede restar una matriz $B$ de orden tres con el número $2$. Lo que tenemos que hacer es pensar que $2X=2IX=2XI=X2I$, donde $I$ es la matriz identidad de orden tres. Recuerda que esta matriz es el elemento neutro de la multiplicación en el conjunto de las matrices cuadradas de orden tres. Entonces:

$$XB–2X=C–AB\Rightarrow XB–X2I=C–AB\Rightarrow X\left(B–2I\right)=C–AB\Rightarrow$$

$$\Rightarrow X\left(B–2I\right){\left(B–2I\right)}^{–1}=\left(C–AB\right){\left(B–2I\right)}^{–1}\Rightarrow X=\left(C–AB\right){\left(B–2I\right)}^{–1}$$

Se tiene que

$$B-2I=\left(\begin{array}{ccc}1& 2& 2\\ 0& 1& 1\\ 1& -1& 2\end{array}\right)=\left(\begin{array}{ccc}2& 0& 0\\ 0& 2& 0\\ 0& 0& 2\end{array}\right)=\left(\begin{array}{ccc}-1& 2& 2\\ 0& -1& 1\\ 1& -1& 0\end{array}\right)$$

Esta matriz tiene inversa ya que su determinante es distinto de cero:

$$\left|\begin{array}{ccc}-1& 2& 2\\ 0& -1& 1\\ 1& -1& 0\end{array}\right|=(0+2+0)-(-2+0+1)=2-(-1)=3$$

La matriz adjunta y la matriz traspuesta de la adjunta de $B-2I$ son, respectivamente, las siguientes:

$$(B-2I{)}^d=\left(\begin{array}{ccc}1& 1& 1\\ -2& -2& 1\\ 4& 1& 1\end{array}\right)\text{;}{((B-2I{)}^d)}^t=\left(\begin{array}{ccc}1& -2& 4\\ 1& -2& 1\\ 1& 1l3& 1\end{array}\right)$$

Por tanto, la matriz inversa de $B-2I$ es:

$$(B-2I{)}^{-1}=\frac{1}{|B-2I|}{((B-2I{)}^t)}^t=\frac{1}{3}\left(\begin{array}{ccc}1& -2& 4\\ 1& -2& 1\\ 1& 1l3& 1\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{3}& -\frac{2}{3}& \frac{4}{3}\\ \frac{1}{3}& -\frac{2}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right)$$

Por otro lado,

$$C-AB=\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\\ 0& 1& 2\end{array}\right)-\left(\begin{array}{ccc}0& 1& 1\\ 0& 2& 1\\ -1& -3& -2\end{array}\right)\left(\begin{array}{ccc}1& 2& 2\\ 0& 1& 1\\ 1& -1& 2\end{array}\right)=$$

$$=\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\\ 0& 1& 2\end{array}\right)-\left(\begin{array}{ccc}-2& -2& -5\\ -1& -1& -1\\ 2& 3& 3\end{array}\right)=\left(\begin{array}{ccc}2& 3& 6\\ 2& 2& 1\\ -2& -2& -1\end{array}\right)$$

Finalmente:

$$X=(C-AB)(B-2I{)}^{-1}=\left(\begin{array}{ccc}2& 3& 6\\ 2& 2& 1\\ -2& -2& -1\end{array}\right)\left(\begin{array}{ccc}\frac{1}{3}& -\frac{2}{3}& \frac{4}{3}\\ \frac{1}{3}& -\frac{2}{3}& \frac{1}{3}\\ \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\end{array}\right)=\left(\begin{array}{ccc}\frac{11}{3}& -\frac{4}{3}& \frac{17}{3}\\ \frac{5}{3}& -\frac{7}{3}& \frac{11}{3}\\ -\frac{5}{3}& \frac{7}{3}& -\frac{11}{3}\end{array}\right)$$

---

Puedes ver y descargar este artículo en formato pdf aquí.

La vida es fascinante; sólo hay que mirarla a través de las gafas correctas

Alejandro Dumas

---

Lo mejor es ver cómo se hace con un ejemplo concreto.

Consideremos la matriz

$$A=\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)$$

El objetivo es hallar una matriz $A^{-1}$ tal que $A{A}^{-1}=A^{-1}A=I$, donde

$$I=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)$$

es la matriz identidad de orden 3. Esta matriz, $A^{-1}$, se llama inversa de $A$.

Lo primero de todo es hallar el determinante de la matriz $A$. Esto es porque hay un teorema que dice que “una matriz cuadrada tiene inversa si, y solo si, su determinante es distinto de cero”. Por tanto, si el determinante de la matriz $A$ es igual a cero, la matriz $A$ no tendrá inversa y se detiene el proceso. Si el determinante no es cero, su valor nos servirá para hallar la inversa de la matriz $A$ usando una fórmula que veremos al final.

Ahora debemos de hallar una matriz, llamada matriz adjunta de la matriz $A$, que la vamos a denominar $A^d$. Esta es una matriz muy peculiar pues cada uno de sus elementos son lo que se llaman adjuntos. Es un proceso puede que, al principio, un poco largo, pero es muy sencillo.

Del primer elemento de la matriz $A$, que es el $a_{11}=2$ vamos a eliminar la fila y la columna donde se encuentra. Observaremos entonces que queda una matriz de orden 2. Fíjate:

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}1& 3\\ 1& 1\end{array}\right)$$

Ahora hallamos el determinante de esta última matriz de orden 2:

$$\left|\begin{array}{cc}1& 3\\ 1& 1\end{array}\right|=1-3=-2\Rightarrow {\mathrm{\Delta }}_{11}=-2$$

El determinante anterior recibe el nombre de menor complementario del elemento $a_{11}$ de la matriz $A$, y como acabas de ver, se escribe con el símbolo ${\mathrm{\Delta }}_{11}$. Cada elemento $a_{ij}$ de la matriz $A$ tendrá su menor complementario ${\mathrm{\Delta }}_{ij}$, que se obtendrá haciendo el determinante de la matriz de orden 2 que resulta de eliminar la fila y la columna donde se encuentra el elemento $a_{ij}$.

Vamos a hallar los ocho menores complementarios restantes. Esto, con el tiempo, lo harás de cabeza, sin necesidad de escribirlos. Imagina, además, la fila y la columna de las que has de prescindir para obtener el correspondiente menor de orden dos.

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}0& 3\\ 2& 1\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{12}=\left|\begin{array}{cc}0& 3\\ 2& 1\end{array}\right|=0-6=-6$$

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}0& 1\\ 2& 1\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{13}=\left|\begin{array}{cc}0& 1\\ 2& 1\end{array}\right|=0-2=-2$$

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{21}=\left|\begin{array}{cc}1& 0\\ 1& 1\end{array}\right|=1-0=1$$

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}2& 0\\ 2& 1\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{22}=\left|\begin{array}{cc}2& 0\\ 2& 1\end{array}\right|=2-0=2$$

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}2& 1\\ 2& 1\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{23}=\left|\begin{array}{cc}2& 1\\ 2& 1\end{array}\right|=2-2=0$$

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}1& 0\\ 0& 3\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{31}=\left|\begin{array}{cc}1& 0\\ 0& 3\end{array}\right|=3-0=3$$

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}2& 0\\ 0& 3\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{32}=\left|\begin{array}{cc}2& 0\\ 0& 3\end{array}\right|=6-0=6$$

$$\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\Rightarrow \left(\begin{array}{cc}2& 1\\ 0& 1\end{array}\right)\Rightarrow {\mathrm{\Delta }}_{33}=\left|\begin{array}{cc}2& 1\\ 0& 1\end{array}\right|=2-0=2$$

Es muy importante andar con sumo cuidado en el cálculo de los menores complementarios sobre todo con la regla de los signos al multiplicar y al restar.

El siguiente paso es hallar el adjunto asociado a cada menor complementario ${\mathrm{\Delta }}_{ij}$, que lo llamaremos $A_{ij}$. Esto es muy sencillo porque los adjuntos son exactamente iguales que los menores complementarios si la suma de su fila y columna es par, y son los menores complementarios cambiados de signo si la suma de su fila y de su columna es impar. Un poco “lioso” de decir pero muy fácil de ver:

$A_{11}={\mathrm{\Delta }}_{11}=-2$. No cambiamos el signo porque $1+1=2$, que es par.

$A_{12}=-{\mathrm{\Delta }}_{12}=-(-6)=6$. Cambiamos el signo porque $1+2=3$, que es impar.

$A_{13}={\mathrm{\Delta }}_{11}=-2$. No cambiamos el signo porque $1+3=4$, que es par.

$A_{21}=-{\mathrm{\Delta }}_{21}=-1$. Cambiamos el signo porque $2+1=3$, que es impar.

$A_{22}={\mathrm{\Delta }}_{22}=2$. No cambiamos el signo porque $2+2=4$, que es par.

$A_{23}=-{\mathrm{\Delta }}_{23}=-0=0$. Cambiamos el signo porque $2+3=5$, que es impar (aunque el cero queda igual).

$A_{31}={\mathrm{\Delta }}_{31}=3$. No cambiamos el signo porque $3+1=4$, que es par.

$A_{32}=-{\mathrm{\Delta }}_{32}=-6$. Cambiamos el signo porque $3+2=5$, que es impar.

$A_{33}={\mathrm{\Delta }}_{33}=2$. No cambiamos el signo porque $3+3=6$, que es par.

Pues bien, hecho esto ya casi hemos terminado. Ahora construimos una matriz, llamada matriz adjunta de la matriz $A$, y que nombraremos así: $A^d$. Los elementos de esta matriz son los adjuntos que hemos hallado anteriormente:

$$A^d=\left(\begin{array}{ccc}{A}_{11}& A_{12}& A_{13}\\ A_{21}& A_{22}& A_{23}\\ A_{31}& A_{32}& A_{33}\end{array}\right)$$

En nuestro ejemplo la matriz adjunta será:

$$A^d=\left(\begin{array}{ccc}-2& 6& -2\\ -1& 2& 0\\ 3& -6& 2\end{array}\right)$$

La matriz inversa de la matriz $A$ viene dada por la siguiente fórmula:

$$A^{-1}=\frac{1}{\left|A\right|}{\left(A^d\right)}^t$$

En la fórmula anterior la matriz ${\left(A^d\right)}^t$ es la traspuesta de la matriz adjunta.

En nuestro ejemplo esta última matriz es

$${\left(A^d\right)}^t=\left(\begin{array}{ccc}-2& -1& 3\\ 6& 2& -6\\ -2& 0& 2\end{array}\right)$$

y, finalmente, la inversa de $A$ será, aplicando la fórmula:

$$A^{-1}=\frac{1}{\left|A\right|}{\left(A^d\right)}^t=\frac{1}{2}\cdot \left(\begin{array}{ccc}-2& -1& 3\\ 6& 2& -6\\ -2& 0& 2\end{array}\right)\Rightarrow A^{-1}=\left(\begin{array}{ccc}-1& -\frac{1}{2}& \frac{3}{2}\\ 3& 1& -3\\ -1& 0& 1\end{array}\right)$$

Ahora se puede hacer la comprobación de que, efectivamente, la inversa está bien hecha:

$$A{A}^{-1}=\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)\left(\begin{array}{ccc}-1& -\frac{1}{2}& \frac{3}{2}\\ 3& 1& -3\\ -1& 0& 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)=I$$

$$A^{-1}A=\left(\begin{array}{ccc}-1& -\frac{1}{2}& \frac{3}{2}\\ 3& 1& -3\\ -1& 0& 1\end{array}\right)\left(\begin{array}{ccc}2& 1& 0\\ 0& 1& 3\\ 2& 1& 1\end{array}\right)=\left(\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right)=I$$

---

Puedes ver y descargar este artículo en formato pdf aquí.

Son capaces, porque creen que son capaces

Virgilio

---

Enunciado

En un rectángulo $ABCD$ de lados 8 cm y 12 cm, se traza desde $B$ una perpendicular a la diagonal $AC$, y desde $D$, otra perpendicular a la misma diagonal. Sean $M$ y $N$ los puntos donde estas perpendiculares cortan a la diagonal. Halla la longitud del segmento $MN$ (ver figura).

Solución

La idea es hallar la diagonal $AC$ y luego hallar $AN=MC$. De este modo tendremos que $MN=AC-2AN$.

En el triángulo $ABC$, que es rectángulo en $B$, por el teorema de Pitágoras, se tiene (ver figura):

$$A{C}^2={12}^2+8^2\Rightarrow A{C}^2=208\Rightarrow AC\cong 14,42\text{cm}$$

En el mismo triángulo anterior también podemos hallar el ángulo $\alpha$, haciendo uso de la tangente:

$$\text{tg}\alpha =\frac{8}{12}\Rightarrow \alpha =\text{arctg}\frac{8}{12}\Rightarrow \alpha =33,69º$$

Para hallar $AN$ vamos a usar el triángulo $AND$, que es rectángulo en $N$ (ver figura siguiente).

En él, está claro que $\beta =90º-\alpha \Rightarrow \beta =90º-33,69º\Rightarrow \beta =56,31º$. Convéncete observando el rectángulo inicial y los dos triángulos anteriores.

Entonces:

$$\cos \beta =\frac{AN}{8}\Rightarrow AN=8\cos 56,31\Rightarrow AN=4,44\text{cm}$$

Finalmente:

$$MN=AC–2AN=14,42–2\cdot 4,44\Rightarrow MN=5,54\text{cm}$$