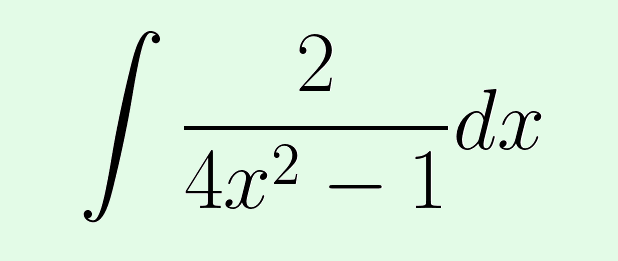integral – matematicastro.es

Conviene aprender hasta del enemigo

Vamos a calcular una primitiva de la función $f (x) = \frac{1}{x^{2} - a^{2}}$ donde $a$ es un número real cualquiera distinto de cero. Es decir, se trata de calcular la integral indefinida $\int \frac{1}{x^{2} - a^{2}} d x$ . Para ello vamos a descomponer en dos fracciones simples la fracción $\frac{1}{x^{2} - a^{2}}$ . Como $x^{2} - a^{2} = (x + a) (x - a)$ , tenemos:

$\frac{1}{x^{2} - a^{2}} = \frac{E}{x + a} + \frac{F}{x - a} = \frac{E (x - a) + F (x + a)}{(x + a) (x - a)} =$

$= \frac{E x - E a + F x + F a}{x^{2} - a^{2}} = \frac{(E + F) x - E a + F a}{x^{2} - a^{2}}$

De aquí se deduce, igualando las fracciones algebraicas primera y última, que

${\begin{cases} E + F = 0 \\ - E a + F a = 1 \end{cases} \Rightarrow {\begin{cases} E = - F \\ 2 F a = 1 \end{cases} \Rightarrow {\begin{cases} E = - \frac{1}{2 a} \\ F = \frac{1}{2 a} \end{cases}$

Es decir:

$\frac{1}{x^{2} - a^{2}} = \frac{- \frac{1}{2 a}}{x + a} + \frac{\frac{1}{2 a}}{x - a}$

Por tanto:

$\int \frac{1}{x^{2} - a^{2}} d x = \int \frac{- \frac{1}{2 a}}{x + a} d x + \int \frac{\frac{1}{2 a}}{x - a} d x =$

$= - \frac{1}{2 a} \int \frac{1}{x + a} d x + \frac{1}{2 a} \int \frac{1}{x - a} d x = - \frac{1}{2 a} \ln | x + a | + \frac{1}{2 a} \ln | x - a | + C =$

$= \frac{1}{2 a} (\ln | x - a | - \ln | x + a |) + C = \frac{1}{2 a} \ln | \frac{x - a}{x + a} | + C$

O sea:

$\int \frac{1}{x^{2} - a^{2}} d x = \frac{1}{2 a} \ln | \frac{x - a}{x + a} | + C (1)$

Ejemplo

Calcular $\int \frac{2}{4 x^{2} - 1} d x$

Solución.

$\int \frac{2}{4 x^{2} - 1} d x = 2 \int \frac{1}{4 x^{2} - 1} d x = 2 \int \frac{\frac{1}{4}}{x^{2} - \frac{1}{4}} d x =$

$= 2 \cdot \frac{1}{4} \int \frac{1}{x^{2} - {(\frac{1}{2})}^{2}} d x = \frac{1}{2} \int \frac{1}{x^{2} - {(\frac{1}{2})}^{2}} d x$

La integral $\int \frac{1}{x^{2} - {(\frac{1}{2})}^{2}} d x$ es del tipo $\int \frac{1}{x^{2} - a^{2}} d x$ con $a = \frac{1}{2}$ . Por tanto, usando la fórmula $(1)$ :

$\int \frac{1}{x^{2} - {(\frac{1}{2})}^{2}} d x = \frac{1}{2 \cdot \frac{1}{2}} \ln | \frac{x - \frac{1}{2}}{x + \frac{1}{2}} | + C = \ln | \frac{2 x - 1}{2 x + 1} | + C$

Entonces:

$\int \frac{2}{4 x^{2} - 1} d x = \frac{1}{2} \int \frac{1}{x^{2} - {(\frac{1}{2})}^{2}} d x = \frac{1}{2} \ln | \frac{2 x - 1}{2 x + 1} | + C$

Archivos de la etiqueta: integral

Una integral racional

Ejemplo