Son capaces, porque creen que son capaces
Enunciado
En un rectángulo $ABCD$ de lados 8 cm y 12 cm, se traza desde $B$ una perpendicular a la diagonal $AC$, y desde $D$, otra perpendicular a la misma diagonal. Sean $M$ y $N$ los puntos donde estas perpendiculares cortan a la diagonal. Halla la longitud del segmento $MN$ (ver figura).
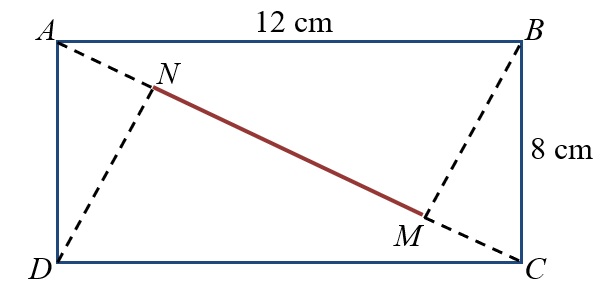
Solución
La idea es hallar la diagonal $AC$ y luego hallar $AN=MC$. De este modo tendremos que $MN=AC-2AN$.
En el triángulo $ABC$, que es rectángulo en $B$, por el teorema de Pitágoras, se tiene (ver figura):
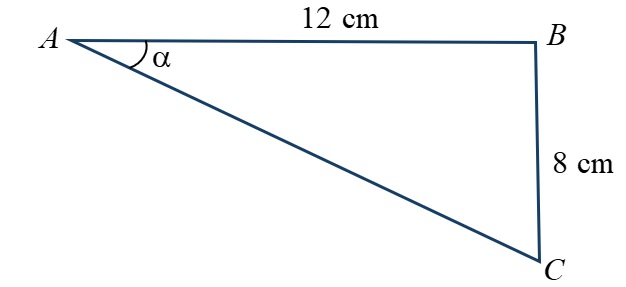
$$AC^2=12^2+8^2\Rightarrow AC^2=208\Rightarrow AC\cong14,42\,\text{cm}$$
En el mismo triángulo anterior también podemos hallar el ángulo $\alpha$, haciendo uso de la tangente:
$$\text{tg}\,\alpha=\frac{8}{12}\Rightarrow\alpha=\text{arctg}\frac{8}{12}\Rightarrow\alpha=33,69º$$
Para hallar $AN$ vamos a usar el triángulo $AND$, que es rectángulo en $N$ (ver figura siguiente).
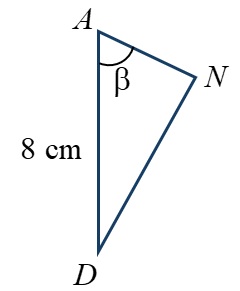
En él, está claro que $\beta=90º-\alpha\Rightarrow\beta=90º-33,69º\Rightarrow\beta=56,31º$. Convéncete observando el rectángulo inicial y los dos triángulos anteriores.
Entonces:
$$\cos \beta = \frac{{AN}}{8} \Rightarrow AN = 8\cos 56,31 \Rightarrow AN = 4,44\,\text{cm}$$
Finalmente:
$$MN = AC – 2AN = 14,42 – 2 \cdot 4,44 \Rightarrow MN = 5,54\,\text{cm}$$
